Positron Annihilation into \(\mu ^+\mu ^-\) Pair in Media

The class G4AnnihiToMuPair simulates the electromagnetic production of muon pairs by the annihilation of high-energy positrons with atomic electrons [eal06]. Details of the implementation are given below and can also be found in Ref. [HBK03].

Total Cross Section

The annihilation of positrons and target electrons producing muon pairs in the final state (\(e^+ e^- \to \mu^+\mu^-\)) may give an appreciable contribution to the total number of muons produced in high-energy electromagnetic cascades. The threshold positron energy in the laboratory system for this process with the target electron at rest is

(141)\[E_{\rm th}=2m_\mu^2/m_e-m_e\approx 43.69\:{\rm GeV}\,,\]

where \(m_\mu\) and \(m_e\) are the muon and electron masses, respectively. Taking into account that the electron is much lighter than the muon, the lowest order cross section can be written in excellent approximation as

(142)\[\sigma=\frac{\pi\,r_\mu^2} 3\, \xi\left(1+\frac\xi2\right) \sqrt{1-\xi}\,,\]

where \(r_\mu=r_e\, m_e/m_\mu\) is the classical muon radius, \(\xi=E_{\rm th}/E\), and \(E\) is the total positron energy in the laboratory frame.

We take into account, that the cross section gets increased by the Sommerfeld-Schwinger-Sakharov (SSS) threshold Coulomb re-summation factor [BL09]:

\[S(\beta)=\frac{X(\beta)}{1-e^{-X(\beta)}} \qquad\]

where

\[\qquad X(\beta) = \frac{\pi \alpha}{\beta \gamma} = \pi \alpha \, \frac{\sqrt{1-\beta^2}}{\beta}\]

The SSS-corrected cross section can be written in good approximation at all energies above threshold as

(143)\[\sigma_{\rm SSS} = \frac{\pi\,r_f^2} 3\, \xi\left(1+\frac\xi2\right) \, \frac{ \pi \alpha \sqrt{\xi}}{1-e^{-\frac{\pi \alpha \sqrt{\xi}}{\sqrt{1-\xi}} }}\;.\]

These expressions are used in the simulation of this process since Geant4 10.5beta. The final factor in the expression is replaced by its asymptotic value of unity very close to threshold to avoid numerical instabilities.

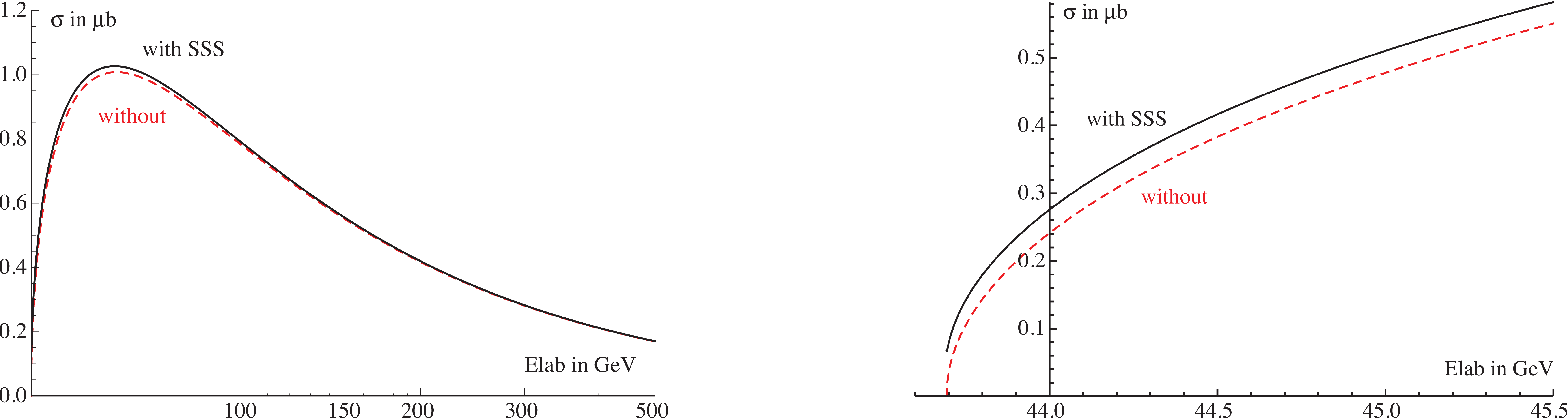
Fig. 30 Total cross section for the process \({\rm e}^+{\rm e}^- \rightarrow \mu^+\mu^-\) as a function of the positron energy \(E\) in the laboratory system. With (solid line) and without (dashed red line) SSS Coulomb re-summation factor, zoomed close to the threshold (left), and using a wider energy range (right)

The cross section as a function of the positron energy \(E\) is shown in Fig. 30. The noticeable increase of the cross section close to threshold by the SSS-factor is of practical interest for the low emittance production of muons, as proposed in reference [BABGarcia+18].

Sampling of Energies and Angles

It is convenient to simulate the muon kinematic parameters in the center-of-mass (c.m.) system, and then to convert into the laboratory frame.

The energies of all particles are the same in the c.m. frame and equal to

(144)\[E_{\rm cm}=\sqrt{\frac12\,m_e(E+m_e)}\,.\]

The muon momenta in the c.m. frame are \(P_{\rm cm}=\sqrt{E_{\rm cm}^2-m_\mu^2}\). In what follows, let the cosine of the angle between the c.m. momenta of the \(\mu^+\) and \(e^+\) be denoted as \(x=\cos\theta_{\rm cm}\) .

From the differential cross section it is easy to derive that, apart from normalization, the distribution in \(x\) is described by

(145)\[f(x)\,d x=(1+\xi+x^2\,(1-\xi))\,d x\,, \quad -1\le x \le1\,.\]

The value of this function is contained in the interval \((1+\xi)\le f(x)\le 2\) and the generation of \(x\) is straightforward using the rejection technique. Fig. 31 shows both generated and analytic distributions.

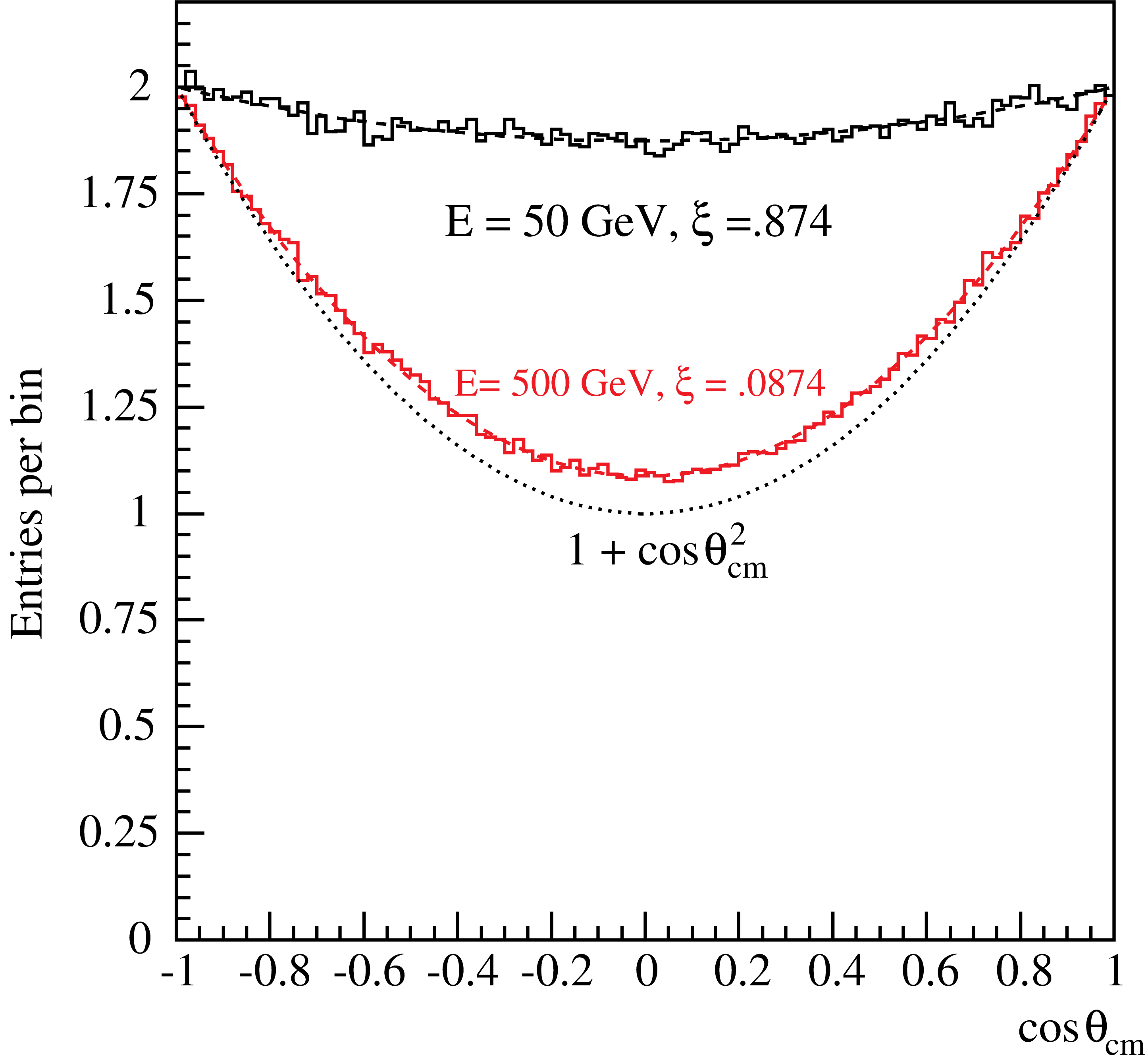
Fig. 31 Generated histograms with \(10^6\) entries each and the expected \(\cos\theta_{\rm cm}\) distributions (dashed lines) at \(E=50\) and 500 GeV positron energy in the lab frame. The asymptotic \(1+\cos\theta_{\rm cm}^2\) distribution valid for \(E \rightarrow \infty\) is shown as dotted line.

The transverse momenta of the \(\mu^+\) and \(\mu^-\) particles are the same, both in the c.m. and the lab frame, and their absolute values are equal to

(146)\[P_\perp=P_{\rm cm} \, \sin\theta_{\rm cm}=P_{\rm cm} \, \sqrt{1-x^2}\,.\]

The energies and longitudinal components of the muon momenta in the lab system may be obtained by means of a Lorentz transformation. The velocity and Lorentz factor of the center-of-mass in the lab frame may be written as

(147)\[\beta=\sqrt{\frac{E-m_e}{E+m_e}}\,,\quad \gamma\equiv\frac1{\sqrt{1-\beta^2}}= \sqrt{\frac{E+m_e}{2 m_e}} = \frac{E_{\rm cm}}{m_e}\,.\]

The laboratory energies and longitudinal components of the momenta of the positive and negative muons may then be obtained:

\[\begin{split}E_+ & = \gamma\,(E_{\rm cm}+x \, \beta \,P_{\rm cm})\,,\quad P_{+_\parallel}=\gamma\,(\beta E_{\rm cm} + x \, P_{\rm cm})\, , \\ E_- & = \gamma\,(E_{\rm cm}-x \, \beta \,P_{\rm cm})\,,\quad P_{-_\parallel}=\gamma\,(\beta E_{\rm cm} - x \, P_{\rm cm})\, .\end{split}\]

Finally, for the vectors of the muon momenta one obtains:

(148)\[\begin{split}{\bf P}_+ &= (+P_\perp\cos\varphi ,+P_\perp \sin\varphi,P_{+_\parallel})\,,\\ {\bf P}_- &= (-P_\perp\cos\varphi, -P_\perp\sin\varphi,P_{-_\parallel})\,,\end{split}\]

where \(\varphi\) is a random azimuthal angle chosen between 0 and \(2\,\pi\). The \(z\)-axis is directed along the momentum of the initial positron in the lab frame.

The maximum and minimum energies of the muons are given by

(149)\[\begin{split}E_{\max} & \approx \frac12\,E\left(1+\sqrt{1-\xi}\right)\,, \\ E_{\min} & \approx \frac12\,E\left(1-\sqrt{1-\xi}\right)= \frac{\displaystyle E_{\rm th}}{\displaystyle 2\left(1+\sqrt{1-\xi} \right)}\,.\end{split}\]

The fly-out polar angles of the muons are approximately

(150)\[\theta_+\approx P_{{}\perp}/P_{+_\parallel},\quad \theta_-\approx P_{{}\perp}/P_{-_\parallel}\,;\]

the maximal angle \(\displaystyle\theta_{\max}\approx\frac{m_e}{m_\mu}\, \sqrt{1-\xi}\) is always small compared to 1.

Validity

The process described is assumed to be purely electromagnetic. It is based on virtual \(\gamma\) exchange, and the \(Z\)-boson exchange and \(\gamma - Z\) interference processes are neglected. The \(Z\)-pole corresponds to a positron energy of \(E = M_Z^2 / 2 m_e = 8136\,{\rm TeV}\). The validity of the current implementation is therefore restricted to initial positron energies of less than about 1000 TeV.

Bibliography

BABGarcia+18

M. Boscolo, M. Antonelli, O. Blanco-Garc’ıa, S. Guiducci, S. Liuzzo, P. Raimondi, and F. Collamati. Low emittance muon accelerator studies with production from positrons on target. Physical Review Accelerators and Beams, jun 2018. URL: https://doi.org/10.1103/physrevaccelbeams.21.061005, doi:10.1103/physrevaccelbeams.21.061005.

BL09

Stanley J. Brodsky and Richard F. Lebed. Production of the smallest QED atom: true muonium ($\mu $$\mathplus $$\mu $-). Physical Review Letters, may 2009. URL: https://doi.org/10.1103/physrevlett.102.213401, doi:10.1103/physrevlett.102.213401.

eal06

A.G. Bogdanov et al. Geant4 simulation of production and interaction of muons. IEEE Trans. Nucl. Sci., 2006.

HBK03

H. Burkhardt, S. Kelner and R. Kokoulin. Production of muon pairs in annihilation of high-energy positrons with resting electrons. CERN-AB-2003-002 (ABP) and CLIC Note 554, January 2003.