Introduction

The abrasion model is a simplified macroscopic model for nuclear-nuclear interactions based largely on geometric arguments rather than detailed consideration of nucleon-nucleon collisions. As such the speed of the simulation is found to be faster than models such as G4BinaryCascade, but at the cost of accuracy. The version of the model implemented is interpreted from the so-called abrasion-ablation model described by Wilson et al. [WTC+95][TWT+93] together with an algorithm from Cucinotta to approximate the secondary nucleon energy spectrum [Cuc94]. By default, instead of performing an ablation process to simulate the de-excitation of the nuclear pre-fragments, the Geant4 implementation of the abrasion model makes use of existing and more detailed nuclear de-excitation models within Geant4 (G4Evaporation, G4FermiBreakup, G4StatMF) to perform this function (see De-excitation of the projectile and target nuclear pre-fragments by standard de-excitation physics). However, in some cases cross sections for the production of fragments with large \(\Delta\)A from the pre-abrasion nucleus are more accurately determined using a Geant4 implementation of the ablation model (see De-excitation of the projectile and target nuclear pre-fragments by nuclear ablation).

The abrasion interaction is the initial fast process in which the overlap region between the projectile and target nuclei is sheered-off (see Fig. 115) The spectator nucleons in the projectile are assumed to undergo little change in momentum, and likewise for the spectators in the target nucleus. Some of the nucleons in the overlap region do suffer a change in momentum, and are assumed to be part of the original nucleus which then undergoes de-excitation.

Less central impacts give rise to an overlap region in which the nucleons can suffer significant momentum change, and zones in the projectile and target outside of the overlap where the nucleons are considered as spectators to the initial energetic interaction.

The initial description of the interaction must, however, take into consideration changes in the direction of the projectile and target nuclei due to Coulomb effects, which can then modify the distance of closest approach compared with the initial impact parameter. Such effects can be important for low-energy collisions.

Initial nuclear dynamics and impact parameter

For low-energy collisions, we must consider the deflection of the nuclei as a result of the Coulomb force (see Fig. 116). Since the dynamics are non-relativistic, the motion is governed by the conservation of energy equation:

\[E_{tot} = \frac{1}{2}\mu \dot r^2 + \frac{{l^2 }}{{2\mu r^2 }} + \frac{{Z_P Z_T e^2 }}{r}\]

where:

\[\begin{split}E_{tot} &= \mbox{total energy in the centre of mass frame;} \\ r, \dot r &= \mbox{distance between nuclei, and rate of change of distance;} \\ l &= \mbox{angular momentum;} \\ \mu &= \mbox{reduced mass of system i.e.} m_1m_2/(m_1+m_2); \\ e &= \mbox{electric charge (units dependent upon the units for } E_{tot} \mbox{ and } r; \\ Z_P, Z_T &= \mbox{charge numbers for the projectile and target nuclei.}\end{split}\]

The angular momentum is based on the impact parameter between the nuclei when their separation is large, i.e.

\[E_{tot} = \frac{1}{2}\frac{{l^2 }}{{\mu b^2 }}\; \Rightarrow \;l{}^2 = 2E_{tot} \mu b^2\]

At the point of closest approach, \(\dot r = 0\), therefore:

\[\begin{split}E_{tot} &= \frac{{E_{tot} b^2 }}{{r^2 }} + \frac{{Z_P Z_T e^2 }}{r} \\ r^2 &= b^2 + \frac{{Z_P Z_T e^2 }}{{E_{tot} }}r\end{split}\]

Rearranging this equation results in the expression:

\[b^2 = r(r - r_m )\]

where:

\[r_m = \frac{{Z_P Z_T e^2 }}{{E_{tot} }}\]

In the implementation of the abrasion process in Geant4, the square of the far-field impact parameter, \(b\), is sampled uniformly subject to the distance of closest approach, \(r\), being no greater than \(r_P\) + \(r_T\) (the sum of the projectile and target nuclear radii).

Abrasion process

In the abrasion process, as implemented by Wilson et al [WTC+95] it is assumed that the nuclear density for the projectile is constant up to the radius of the projectile (\(r_P\)) and zero outside. This is also assumed to be the case for the target nucleus. The amount of nuclear material abraded from the projectile is given by the expression:

\[\Delta _{abr} = FA_P \left[ {1 - \exp \left( { - \frac{{C_T }}{\lambda }} \right)} \right]\]

where F is the fraction of the projectile in the interaction zone, \(\lambda\) is the nuclear mean-free-path, assumed to be:

\[\lambda = \frac{{16.6}}{{E^{0.26} }}\]

\(E\) is the energy of the projectile in MeV/nucleon and \(C_T\) is the chord-length at the position in the target nucleus for which the interaction probability is maximum. For cases where the radius of the target nucleus is greater than that of the projectile (i.e. \(r_T > r_P\)):

\[\begin{split}C_T = \left\{ {\begin{array}{cc} {2\sqrt {r_T^2 - x^2 } } & {:x > 0} \\ {2\sqrt {r_T^2 - r^2 } } & {:x \le 0} \\ \end{array}} \right.\end{split}\]

where:

\[x = \frac{{r_P^2 + r^2 - r_T^2 }}{{2r}}\]

In the event that \(r_P > r_T\) then \(C_T\) is:

\[\begin{split}C_T = \left\{ {\begin{array}{cc} {2\sqrt {r_T^2 - x^2 } } & {:x > 0} \\ {2r_T } & {:x \le 0} \\ \end{array}} \right.\end{split}\]

where:

\[x = \frac{{r_T^2 + r^2 - r_P^2 }}{{2r}}\]

The projectile and target nuclear radii are given by the expression:

\[\begin{split}r_P &\approx 1.29\sqrt {r_{RMS,P}^2 - 0.84^2 } \\ r_T &\approx 1.29\sqrt {r_{RMS,T}^2 - 0.84^2 }\end{split}\]

The excitation energy of the nuclear fragment formed by the spectators in the projectile is assumed to be determined by the excess surface area, given by:

\[\Delta S = 4\pi r_P^2 \left[ 1 + P - \left( {1 - F} \right)^{2/3} \right]\]

where the functions \(P\) and \(F\) are given in section [PandF]. Wilson et al equate this surface area to the excitation to:

\[E_S = 0.95\Delta S\]

if the collision is peripheral and there is no significant distortion of the nucleus, or

\[\begin{split} E_S & = 0.95\left\{ {1 + 5F + \Omega F^3 } \right\}\Delta S \\ \Omega & = \left\{ {\begin{array}{rl} 0 & :A_P > 16 \\ 1500 & :A_P < 12 \\ 1500 - 320 (A_P -12 ) & : 12 \le A_P \le 16 \\ \end{array}} \right.\end{split}\]

if the impact separation is such that \(r \ll r_P\)+\(r_T\). \(E_S\) is in MeV provided \(\Delta S\) is in fm\(^2\).

For the abraded region, Wilson et al assume that fragments with a nucleon number of five are unbounded, 90% of fragments with a nucleon number of eight are unbound, and 50% of fragments with a nucleon number of nine are unbound. This was not implemented within the Geant4 version of the abrasion model, and disintegration of the pre-fragment was only simulated by the subsequent de-excitation physics models in the G4DeexcitationHandler (evaporation, etc. or G4WilsonAblationModel) since the yields of lighter fragments were already underestimated compared with experiment.

In addition to energy as a result of the distortion of the fragment, some energy is assumed to be gained from transfer of kinetic energy across the boundaries of the nuclei. This is approximated to the average energy transferred to a nucleon per unit intersection pathlength (assumed to be 13 MeV/fm) and the longest chord-length, \(C_l\), and for half of the nucleon-nucleon collisions it is assumed that the excitation energy is:

\[\begin{split}E_X^* = \left\{ \begin{array}{rl} 13 \cdot \left[ 1+\frac{C_t - 1.5}{3} \right] C_l & :C_t > 1.5 \mbox{ fm} \\ 13 \cdot C_l & :C_t \le 1.5\mbox{ fm} \\ \end{array} \right.\end{split}\]

where:

\[\begin{split}C_l = \left\{ \begin{array}{rl} 2\sqrt {r_P^2 + 2rr_T - r^2 - r_T^2 } & r > r_T \\ 2r_P & r \le r_T \\ \end{array} \right.\end{split}\]

\[C_t = 2\sqrt {r_P^2 - \frac{{\left( {r_P^2 + r^2 - r_T^2 } \right)^2 }}{{4r^2 }}}\]

For the remaining events, the projectile energy is assumed to be unchanged. Wilson et al assume that the energy required to remove a nucleon is 10 MeV, therefore the number of nucleons removed from the projectile by ablation is:

\[\Delta _{abl} = \frac{{E_S + E_X }}{{10}} + \Delta _{spc}\]

where \(\Delta _{spc}\) is the number of loosely-bound spectators in the interaction region, given by:

\[\Delta _{spc} = A_P F\exp \left( { - \frac{{C_T }}{\lambda }} \right)\]

Wilson et al appear to assume that for half of the events the excitation energy is transferred into one of the nuclei (projectile or target), otherwise the energy is transferred in to the other (target or projectile respectively).

The abrasion process is assumed to occur without preference for the nucleon type, i.e. the probability of a proton being abraded from the projectile is proportional to the fraction of protons in the original projectile, therefore:

\[\Delta Z_{abr} = \Delta _{abr} \frac{{Z_P }}{{A_P }}\]

In order to calculate the charge distribution of the final fragment, Wilson et al assume that the products of the interaction lie near to nuclear stability and therefore can be sampled according to the Rudstam equation (see De-excitation of the projectile and target nuclear pre-fragments by nuclear ablation). The other obvious condition is that the total charge must remain unchanged.

Abraded nucleon spectrum

Cucinotta has examined different formulae to represent the secondary protons spectrum from heavy ion collisions [Cuc94]. One of the models (which has been implemented to define the final state of the abrasion process) represents the momentum distribution of the secondaries as:

\[\psi (p) \propto \sum\limits_{i = 1}^3 {C_i \exp \left( - \frac{p^2}{2p_i^2} \right)} + d_0 \frac{\gamma p}{\sinh \left( {\gamma p} \right)}\]

where:

\[\begin{split}\psi (p) &= \mbox{number of secondary protons with momentum } p \\ & \qquad \mbox{per unit of momentum phase space} [c^3/\mbox{MeV}^3]; \\ p &= \mbox{magnitude of the proton momentum in the rest frame} \\ & \qquad \mbox{of the nucleus from which the particle is projected [MeV/c]}; \\ C_1, C_2, C_3 &= 1.0, 0.03, \mbox{ and } 0.0002; \\ p_1, p_2, p_3 &= \sqrt{2/5} , \sqrt{6/5} p_F, 500 [\mbox{MeV}/c] \\ p_F &= \mbox{Momentum of nucleons in the nuclei at the Fermi surface } [\mbox{MeV}/c] \\ d_0 &= 0.1 \\ \frac{1}{\gamma} &= 90 [\mbox{MeV}/c] ;\end{split}\]

G4WilsonAbrasionModel approximates the momentum distribution for the neutrons to that of the protons, and as mentioned above, the nucleon type sampled is proportional to the fraction of protons or neutrons in the original nucleus.

The angular distribution of the abraded nucleons is assumed to be isotropic in the frame of reference of the nucleus, and therefore those particles from the projectile are Lorentz-boosted according to the initial projectile momentum.

De-excitation of the projectile and target nuclear pre-fragments by standard Geant4 de-excitation physics

Unless specified otherwise, G4WilsonAbrasionModel will instantiate the following de-excitation models to treat subsequent particle emission of the excited nuclear pre-fragments (from both the projectile and the target):

1. G4Evaporation, which will perform nuclear evaporation of (\(\alpha\)-particles, ³He, ³H, ²H, protons and neutrons, in competition with photo-evaporation and nuclear fission (if the nucleus has sufficiently high A).

2. G4FermiBreakUp, for nuclei with \(A \le\) 12 and \(Z \le\) 6.

3. G4StatMF, for multi-fragmentation of the nucleus (minimum energy for this process set to 5 MeV).

As an alternative to using this de-excitation scheme, the user may provide to the G4WilsonAbrasionModel a pointer to her own de-excitation handler, or invoke instantiation of the ablation model (G4WilsonAblationModel).

De-excitation of the projectile and target nuclear pre-fragments by nuclear ablation

A nuclear ablation model, based largely on the description provided by Wilson et al [WTC+95], has been developed to provide a better approximation for the final nuclear fragment from an abrasion interaction. The algorithm implemented in G4WilsonAblationModel uses the same approach for selecting the final-state nucleus as NUCFRG2 and determining the particles evaporated from the pre-fragment in order to achieve that state. However, use is also made of classes in Geant4‘s evaporation physics to determine the energies of the nuclear fragments produced.

The number of nucleons ablated from the nuclear pre-fragment (whether as nucleons or light nuclear fragments) is determined based on the average binding energy, assumed by Wilson et al to be 10 MeV, i.e.:

\[\begin{split}A_{abl} = \left\{ \begin{array}{rl} \mbox{Int} \left( \frac{E_x}{10\mbox{MeV}} \right) & :A_{PF} > \mbox{Int}\left( {\frac{E_x}{10\mbox{MeV}}} \right) \\ A_{PF} & : \mbox{otherwise} \\ \end{array} \right.\end{split}\]

Obviously, the nucleon number of the final fragment, \(A_F\), is then determined by the number of remaining nucleons. The proton number of the final nuclear fragment (\(Z_F\)) is sampled stochastically using the Rudstam equation:

\[\sigma (A_F ,Z_F ) \propto \exp \left( - R\left| {Z_F - SA_F - TA_F^2 } \right|^{3/2} \right)\]

Here \(R = 11.8/AF^{0.45}\), \(S =0.486\), and \(T =3.8 \cdot 10^{-4}\). Once \(Z_F\) and \(A_F\) have been calculated, the species of the ablated (evaporated) particles are determined again using Wilson’s algorithm. The number of \(\alpha\)-particles is determined first, on the basis that these have the greatest binding energy:

\[\begin{split}N_\alpha = \left\{ \begin{array}{cc} {\mbox{Int}\left( \frac{Z_{abl}}{2} \right)} & : \mbox{Int}\left( \frac{Z_{abl}}{2} \right) < \mbox{Int}\left( \frac{A_{abl}}{4} \right) \\ {\mbox{Int}\left( \frac{A_{abl}}{4} \right)} & : \mbox{Int}\left( \frac{Z_{abl}}{2} \right) \ge \mbox{Int}\left( \frac{A_{abl}}{4} \right) \\ \end{array} \right.\end{split}\]

Calculation of the other ablated nuclear/nucleon species is determined in a similar fashion in order of decreasing binding energy per nucleon of the ablated fragment, and subject to conservation of charge and nucleon number.

Once the ablated particle species are determined, use is made of the Geant4 evaporation classes to sample the order in which the particles are ejected (from G4AlphaEvaporationProbability, G4He3EvaporationProbability, G4TritonEvaporationProbability, G4DeuteronEvaporationProbability, G4ProtonEvaporationProbability and G4NeutronEvaporationProbability) and the energies and momenta of the evaporated particle and the residual nucleus at each two-body decay (using G4AlphaEvaporationChannel, G4He3EvaporationChannel, G4TritonEvaporationChannel, G4DeuteronEvaporationChannel, G4ProtonEvaporationChannel and G4NeutronEvaporationChannel). If at any stage the probability for evaporation of any of the particles selected by the ablation process is zero, the evaporation is forced, but no significant momentum is imparted to the particle/nucleus. Note, however, that any particles ejected from the projectile will be Lorentz boosted depending upon the initial energy per nucleon of the projectile.

Definition of the functions P and F used in the abrasion model

In the first instance, the form of the functions \(P\) and \(F\) used in the abrasion model are dependent upon the relative radii of the projectile and target and the distance of closest approach of the nuclear centres. Four radius condtions are treated:

• Case 1, where \(r_T > r_P\) and \(r_T-r_P \leq r \leq r_T + r_P\):

  \[\begin{split}P &= 0.125\sqrt {\mu \nu } \left( {\frac{1}{\mu } - 2} \right)\left( {\frac{{1 - \beta }}{\nu }} \right)^2 - 0.125\left[ {0.5\sqrt {\mu \nu } \left( {\frac{1}{\mu } - 2} \right) + 1} \right]\left( {\frac{{1 - \beta }}{\nu }} \right)^3 \\ F &= 0.75\sqrt {\mu \nu } \left( {\frac{{1 - \beta }}{\nu }} \right)^2 - 0.125\left[ {3\sqrt {\mu \nu } - 1} \right]\left( {\frac{{1 - \beta }}{\nu }} \right)^3\end{split}\]

  where:

  \[\begin{split}\nu &= \frac{{r_P }}{{r_P + r_T }} \\ \beta &= \frac{r}{{r_P + r_T }} \\ \mu &= \frac{{r_T }}{{r_P }}\end{split}\]

• Case 2, where \(r_T > r_P\) and \(r < r_T-r_P\):

  \[\begin{split}P &= - 1 \\ F & = 1\end{split}\]

• Case 3, where \(r_P > r_T\) and \(r_P - r_T \leq r \leq r_P + r_T\):

  \[\begin{split}P &= 0.125\sqrt {\mu \nu } \left( \frac{1}{\mu} - 2 \right) \left( \frac{1 - \beta }{\nu} \right)^2 - 0.125\left\{ 0.5\sqrt \frac{\nu}{\mu} \left( \frac{1}{\mu} - 2 \right) - \left[ \frac{\sqrt {1- \mu^2}}{\nu} -1 \right] \sqrt \frac{2-\mu}{\mu^5} \right\}\left( \frac{1-\beta}{\nu}\right)^3 \\ F &= 0.75\sqrt{\mu \nu} \left(\frac{1-\beta}{\nu} \right)^2 - 0.125\left[ 3\sqrt{\frac{\nu}{\mu}} - \frac{\left[1- (1-\mu^2)^{3/2} \right] \sqrt{1-(1-\mu)^2}}{\mu^3} \right] \left( \frac{1 -\beta}{\nu} \right)^3\end{split}\]

• Case 4, where \(r_P>r_T\) and \(r < r_T-r_P\):

  \[\begin{split}P &= \left[ \frac{\sqrt {1- \mu^2}}{\nu} - 1 \right]\sqrt{1- \left( \frac{\beta }{\nu} \right)^2 } \\ F &= \left[ 1 - \left( 1- \mu^2 \right)^{3/2} \right]\sqrt 1 - \left( \frac{\beta}{\nu} \right)^2\end{split}\]

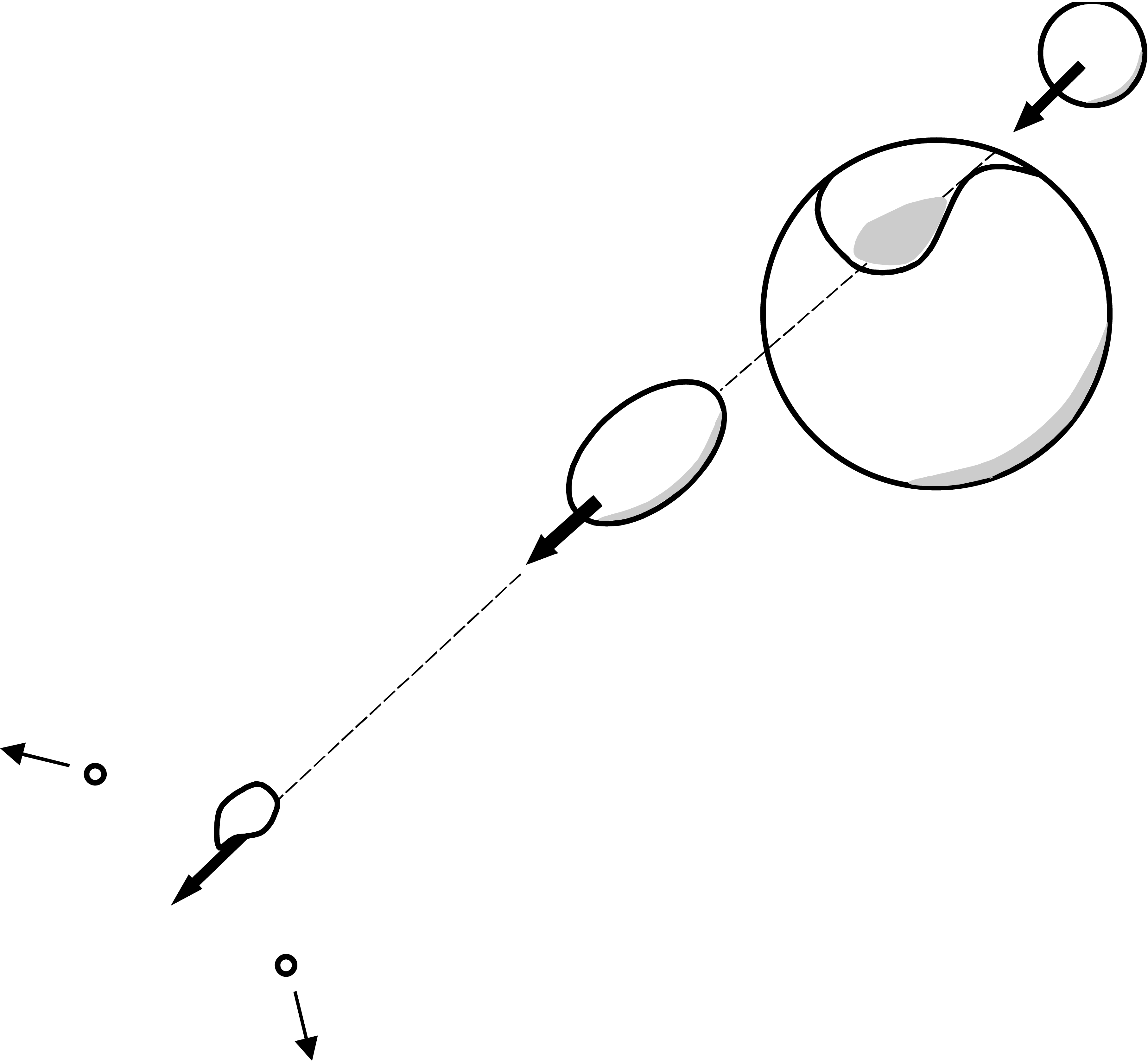
Fig. 115 In the abrasion process, a fraction of the nucleons in the projectile and target nucleons interact to form a fireball region with a velocity between that of the projectile and the target. The remaining spectator nucleons in the projectile and target are not initially affected (although they do suffer change as a result of longer-term de-excitation).

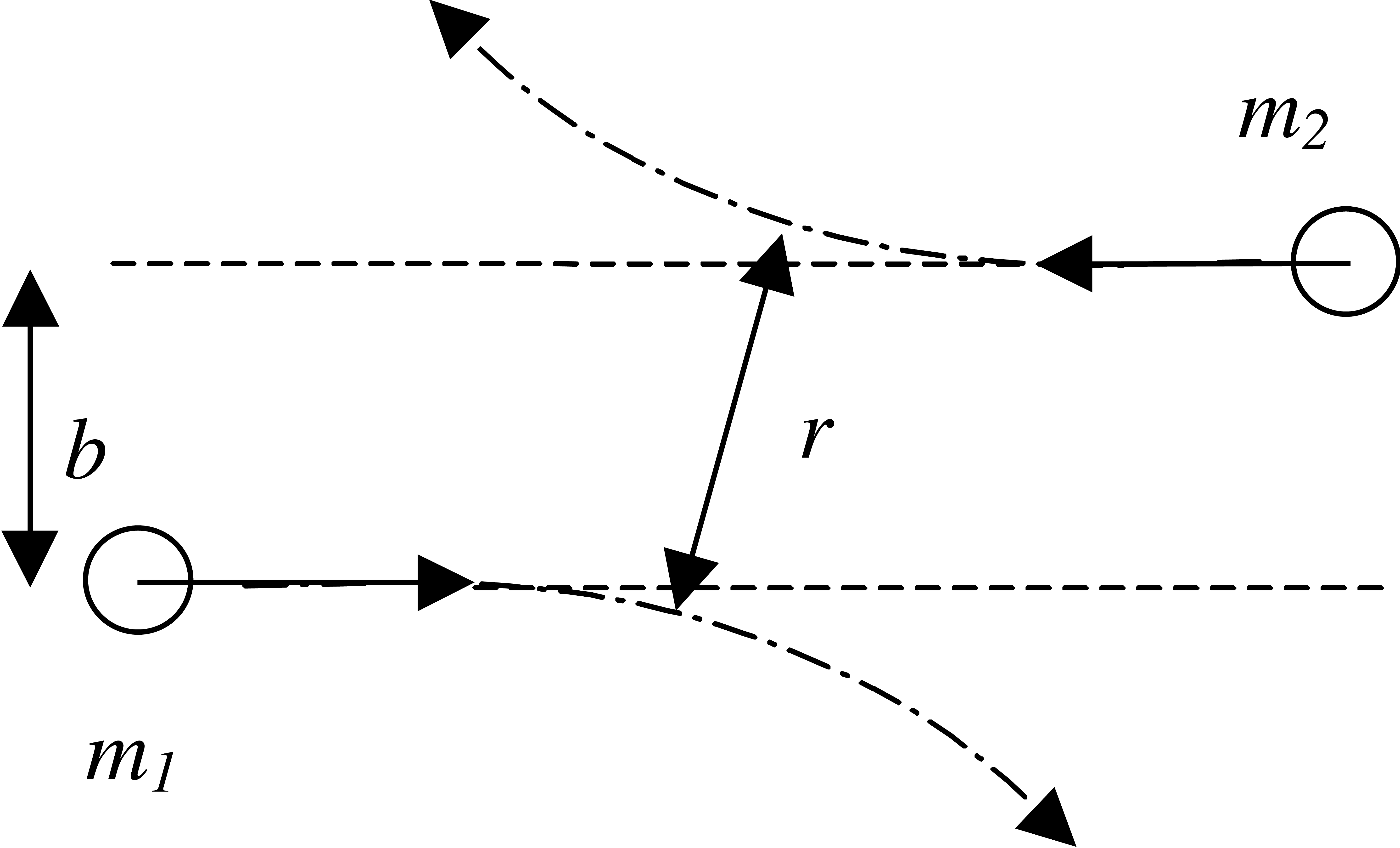
Fig. 116 Illustration clarifying impact parameter in the far-field (\(b\)) and actual impact parameter (\(r\)).

Bibliography

Cuc94(1,2)

Francis A Cucinotta. Multiple-scattering model for inclusive proton production in heavy ion collisions. Technical Report 3470, NASA Technical Paper, 1994.

TWT+93

Lawrence W Townsend, John W Wilson, Ram K Tripathi, John W Norbury, Francis F Badavi, and and Ferdou Khan. Hzefrg1, an energy-dependent semiempirical nuclear fragmentation model. Technical Report 3310, NASA Technical Paper, 1993.

WTC+95(1,2,3)

J W Wilson, R K Tripathi, F A Cucinotta, J K Shinn, F F Badavi, S Y Chun, J W Norbury, C J Zeitlin, L Heilbronn, and and J Miller. Nucfrg2: an evaluation of the semiempirical nuclear fragmentation database. Technical Report 3533, NASA Technical Paper, 1995.