Introduction

Phonons are quantized vibrations in solid-state lattices or amorphous solids, of interest to the low-temperature physics community. Phonons are typically produced when a heat source excites lattice vibrations, or when energy from radiation is deposited through elastic interactions with nuclei of lattice atoms. Below 1 K, thermal phonons are highly suppressed; this leaves only acoustic and optical phonons to propagate.

There is significant interest from the condensed-matter community and direct dark-matter searches to integrate phonon production and propagation with the excellent nuclear and electromagnetic simulations available in Geant4. An effort in this area began in 2011 by the SuperCDMS Collaboration [BAB+12] and is continuing; initial developments in phonon propagation have been incorporated into the Geant4 toolkit for Release 10.0.

As quasiparticles, phonons at low temperatures may be treated in the Geant4 particle-tracking framework, carrying well defined momenta, and propagating in specific directions until they interact [BAB+12]. The present implementation handles ballistic transport, scattering with mode-mixing, and anharmonic downconversion [Tam93a][Tam93b][Tam85] of acoustic phonons. Optical phonon transport and interactions between propagating phonons and thermal background phonons are not treated.

Production of phonons from charged particle energy loss or by photon-lattice interactions are in development, but are not yet included in the Geant4 toolkit.

Phonon Propagation

The propagation of phonons is governed by the three-dimensional wave equation [Wol98]:

(291)\[\rho \omega ^2e_i=C_{ijlm}k_jk_me_l\]

where \(\rho\) is the crystal mass density and \(C_{ijml}\) is the elasticity tensor; the phonon is described by its wave vector \(\vec{k}\), frequency \(\omega\) and polarization \(\vec{e}\).

For a given wave vector \(\vec{k}\), Eq.(291) has three eigenvalues \(\omega\) and three polarization eigenvectors \(\vec{e}\). The three polarization states are labelled Fast Transverse (FT), Slow Transverse (ST) and Longitudinal (L). The direction and speed of propagation of the phonon are given by the group velocity \(\vec{v_g} = d\omega/dk\), which may be computed from Eq.(291):

(292)\[\vec{v_g}=\frac{d \omega (\vec{k})}{d\vec{k}}=\nabla_k \omega (\vec{k})\ .\]

Since the lattice tensor \(C_{ijml}\) is anisotropic in general, the phonon group velocity \(\vec{v_g}\) is not parallel to the momentum vector \(\hbar\vec{k}\). This anisotropic transport leads to a focussing effect, where phonons are driven to directions which correspond to the highest density of eigenvectors \(\vec{k}\). Experimentally, this is seen [NW79] as caustics in the energy distribution resulting from a point-like phonon source isotropic in \(\vec{k}\)-space, as shown in Fig. 122.

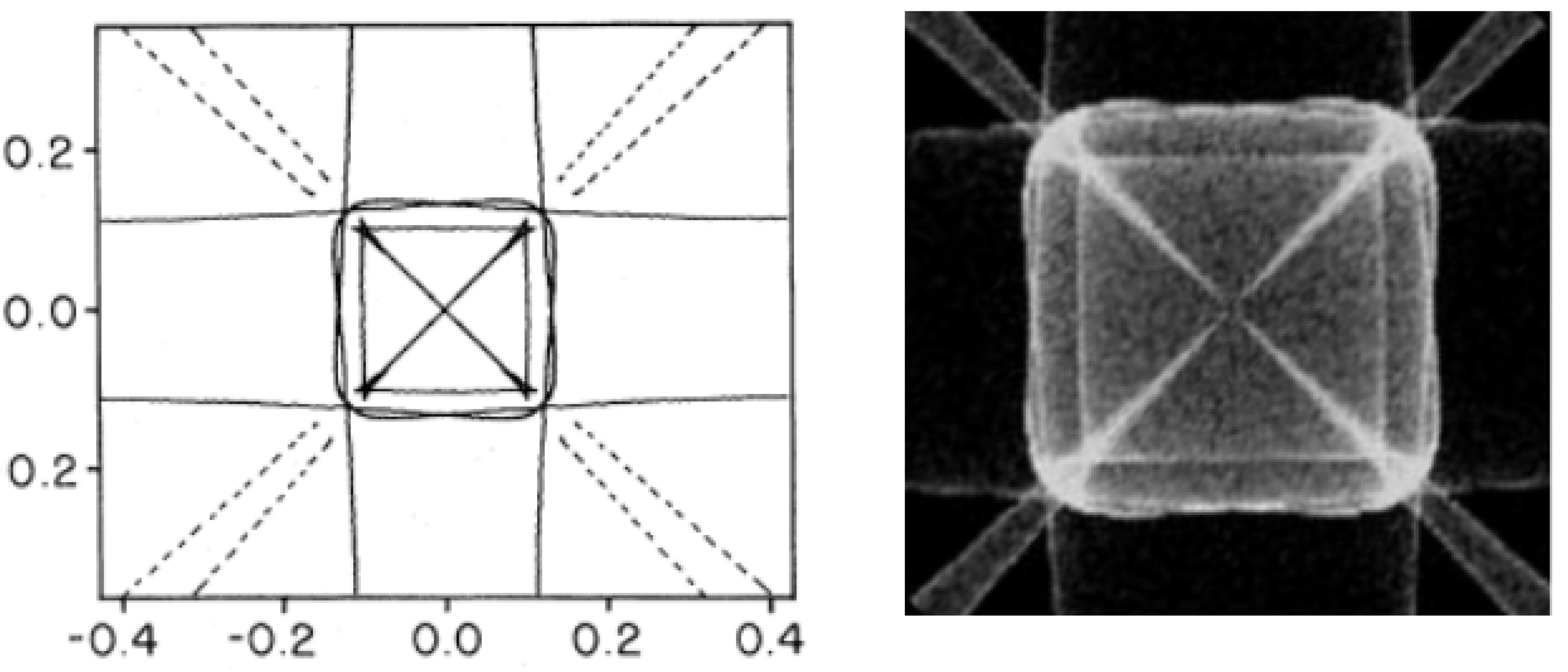
Fig. 122 Left: outline of phonon caustics in germanium as predicted by Northrop and Wolfe [NW79]. Right: Phonon caustics as simulated using the Geant4 phonon transport code.

Lattice Parameters

Scattering and Mode Mixing

In a pure crystal, isotope scattering occurs when a phonon interacts with an isotopic substitution site in the lattice. We treat it as an elastic scattering process, where the phonon momentum direction (wave vector) and polarization are both randomized. The scattering rate for a phonon of frequency \(\nu\) (\(\omega/2\pi\)) is given by [Tam93b]

(293)\[\Gamma_{scatter} = B\nu^4\]

where \(\Gamma_{scatter}\) is the number of scattering events per unit time, and \(B\) is a constant of proportionality derived from the elasticity tensor (see Eq. 11 and Table 1 in [Tam85]). For germanium, \(B = 3.67 \times 10^{-41} \mbox{s}^3\). [Tam85]

At each scattering event, the phonon polarization may change between any of the three states \(L\), \(ST\), \(FT\). The branching ratios for the polarizations are determined by the relative density of allowed states in the lattice. This process is often referred to as mode mixing.

Anharmonic Downconversion

An energetic phonon may interact in the crystal to produce two phonons of reduced energy. This anharmonic downconversion conserves energy (\(\vec{k} = \vec{k}' + \vec{k}''\)), but not momentum, since momentum is exchanged with the bulk lattice. In principle, all three polarization states may decay through downconversion. In practice, however, the rate for \(L\)-phonons completely dominates the energy evolution of the system, with downconversion events from other polarization states being negligible [Tam93b].

The total downconversion rate \(\Gamma_{anh}\) for an \(L\)-phonon of frequency \(\nu\) is given by [Tam93b]

(294)\[\Gamma_{anh} = A\nu^5\]

where (as in Eq.(293)) \(A\) is a constant of proportionality derived from the elasticity tensor (see Eq. 11 and Table 1 in [Tam85]). For germanium, \(A = 6.43 \times 10^{-55} \mbox{s}^4\). [Tam85]

Downconversion may produce either two transversely polarized phonons, or one transverse and one longitudinal. The relative rates are determined by dynamical constants derived from the elasticity tensor \(C_{ijkl}\).

As can be seen from Eqs.(293) and (294), phonon interactions depend strongly on energy \(\hbar\nu\). High energy phonons (\(\nu \sim\) THz) start out in a diffusive regime with high isotope scattering and downconversion rates and mean free paths of order microns. After several such interactions, mean free paths increase to several centimeters or more. This transition from a diffuse to a ballistic transport mode is commonly referred to as “quasi-diffuse” and it controls the time evolution of phonon heat pulses.

Simulation of heat pulse propagation using our Geant4 transport code has been described previously [BAB+12] and shows good agreement with experiment.

Bibliography

BAB+12(1,2,3)

D. Brandt, M. Asai, P. L. Brink, B. Cabrera, E. do Couto e Silva, M. Kelsey, S. W. Leman, K. McArthy, R. Resch, D. Wright, and E. Figueroa-Feliciano. Monte carlo simulation of massive absorbers for cryogenic calorimeters. Journal of Low Temperature Physics, 167(3-4):485–490, feb 2012. URL: https://doi.org/10.1007/s10909-012-0480-3, doi:10.1007/s10909-012-0480-3.

NW79(1,2)

G. A. Northrop and J. P. Wolfe. Ballistic phonon imaging in solids—a new look at phonon focusing. Physical Review Letters, 43(19):1424–1427, nov 1979. URL: https://doi.org/10.1103/PhysRevLett.43.1424, doi:10.1103/physrevlett.43.1424.

Tam93a

S. Tamura. Monte carlo calculations of quasidiffusion in silicon. Journal of Low Temperature Physics, 93(3-4):433–438, nov 1993. URL: https://doi.org/10.1007/BF00693457, doi:10.1007/bf00693457.

Tam85(1,2,3,4,5)

Shin-ichiro Tamura. Spontaneous decay rates of LA phonons in quasi-isotropic solids. Physical Review B, 31(4):2574–2577, feb 1985. URL: https://doi.org/10.1103/PhysRevB.31.2574, doi:10.1103/physrevb.31.2574.

Tam93b(1,2,3,4)

Shin-ichiro Tamura. Quasidiffusive propagation of phonons in silicon: monte carlo calculations. Physical Review B, 48(18):13502–13507, nov 1993. URL: https://doi.org/10.1103/PhysRevB.48.13502, doi:10.1103/physrevb.48.13502.

Wol98

J.P. Wolfe. Imaging Phonons, Chapter 2. Cambridge University Press, United Kingdom, 1998.