Next: Variables
Up: Conventions
Previous: Elements which do not
Contents
Index
Sign Conventions for Magnetic Fields
The MAD program uses the following Taylor expansion for the normal and
skewed field components respectively in the mid-plane  =0,
described in SLAC-75:
=0,
described in SLAC-75:

Note the factorial in the denominator.
The field coefficients have the following meaning:
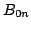
- Normal dipole field component.
The component is positive, if the field points in positive
 direction.
A positive field bends a positively charged particle travelling in
positive
direction.
A positive field bends a positively charged particle travelling in
positive  -direction to the right.
-direction to the right.

- Skew dipole field component.
The component is positive, if the field points in negative
 direction.
A positive field bends a positively charged particle travelling in
positive
direction.
A positive field bends a positively charged particle travelling in
positive  -direction down.
-direction down.

- Normal quadrupole field component
 .
The component is positive, if
.
The component is positive, if  is positive on the positive
is positive on the positive  -axis.
A positive value corresponds to horizontal focussing of a positively
charged particle.
-axis.
A positive value corresponds to horizontal focussing of a positively
charged particle.

- Skew quadrupole field component
 .
The component is positive, if
.
The component is positive, if  is negative on the positive
is negative on the positive  -axis.
-axis.

- Normal sextupole field component
 .
The component is positive, if
.
The component is positive, if  is positive on the
is positive on the  -axis.
-axis.

- Skew sextupole field component
 .
The component is negative, if
.
The component is negative, if  is positive on the
is positive on the  -axis.
-axis.

- Normal octupole field component
 .
The component is positive, if
.
The component is positive, if  is positive on the positive
is positive on the positive  -axis.
-axis.

- Skew octupole field component
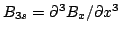 .
The component is negative, if
.
The component is negative, if  is positive on the
is positive on the  -axis.
-axis.
All derivatives are taken on the  -axis.
Using this expansion and the curvature
-axis.
Using this expansion and the curvature  of the reference orbit,
the longitudinal component of the vector potential for a magnet with
mid-plane symmetry is to order 4:
of the reference orbit,
the longitudinal component of the vector potential for a magnet with
mid-plane symmetry is to order 4:

Taking
 in curvilinear coordinates,
the field components can be computed as
in curvilinear coordinates,
the field components can be computed as
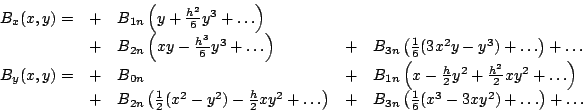
One can easily verify that both
 and
and
 are zero to the order of the
are zero to the order of the  term.
Introducing the magnetic rigidity
term.
Introducing the magnetic rigidity  ,
the multipole coefficients are computed as
,
the multipole coefficients are computed as

Note that the  have the same sign as the corresponding
field components
have the same sign as the corresponding
field components  .
The signs will be changed due to the sign of particle charges and
the direction of travel of the beam.
.
The signs will be changed due to the sign of particle charges and
the direction of travel of the beam.





Next: Variables
Up: Conventions
Previous: Elements which do not
Contents
Index
MAD User Guide, http://wwwslap.cern.ch/mad/