Spin Maps Concatenation

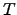So if $T$ is a spin map, it is then given by a couple of objects:

$$T= \left({m,S}\right)$$ (11.8)

where 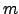$m$ is an orbital map and 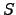$S$ is an orbital dependent spin matrix. If a beam line #1 is followed by beam line #2, then the spin map for the full beam line is given by:

$${T}_{2}\circ {T}_{1} = \left({{m}_{2},{S}_{2}}\right)\circ \left({{m}_{1},{S}_{1}}\right)$$

$$= \left({{m}_{2}\circ {m}_{1},{S}_{2}\circ {m}_{1}{S}_{1}}\right)$$ (11.9)

The matrix 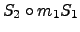${S}_{2}\circ {m}_{1}{S}_{1}$ is simply the product of $S_2 S_1$ where $S_2(\overline{z})$ is evaluated at $\overline{z}=m_2(z)$ with $z=(x,p_x,y,p_y,z_5,z_6)$.