Factoring the Map $T$ and the invariant spin axis $\vec{n}$

The map $U$ can be conveniently factorized as follows:

$$U= \left({{a}_{1},I}\right)\circ \left({I,A}\right)\circ \left({{a}_{\ell},I}\right)\circ \left({{a}_{n\ell},I}\right)$$ (11.11)

The total map 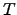$T$ is thus given

$$T = \left({m,S}\right)$$

$$= \left({{a}_{1},I}\right)\circ \underbrace{\left({I,A}\right)\circ... ...size$~=~\left({{m}_{f},{S}_{f}}\right)$}}^{}\circ \left({{a}_{1}^{-1},I}\right)$$ (11.12)

First, let us ignore the transformation $\left({{a}_{1},I}\right)$; this transformation brings us to a parameter dependent system, i.e., it does not tell us how the system is but how the system would be if we changed some parameters, for example quadrupole strengths. Therefore let us look at the map:

$${T}_{f} = ~\left({{m}_{f},{S}_{f}}\right)$$

$$= \underbrace{\left({I,A}\right)\circ \overbrace{\overbrace{\left({... ...}{\rm i}{\rm n}{\rm t}\mbox{\normalsize$~=~\left({{m}_{f},{S}_{f}}\right)$}}^{}$$ (11.13)

This map is truly the map used by the tracking code. We will consider the following map

$${T}_{f}\circ \left({I,A}\right)$$ (11.14)

computed two different ways. First, we use the obvious ways:

$${T}_{f}\circ \left({I,A}\right) = \left({{m}_{f},{S}_{f}}\right)\circ \left({I,A}\right)$$

$$= \left({{m}_{f},{S}_{f}A}\right)$$ (11.15)

Now, let us use the normal form representation of Eq. (11.13) and rewrite Eq. (11.15):

$${T}_{f}\circ \left({I,A}\right) = \left({I,A}\right)\circ \left({{m}_{f},{e}^{\theta \circ {a}_{f}^{-1}{L}_{y}}}\right)\circ \left({I,{A}^{-1}}\right)\circ \left({I,A}\right)$$

$$= \left({I,A}\right)\circ \left({{m}_{f},{e}^{\theta \circ {a}_{f}^{-1}{L}_{y}}}\right)$$

$$= \left({{m}_{f},A\circ {m}_{f}{e}^{\theta \circ {a}_{f}^{-1}{L}_{y}}}\right)$$ (11.16)

Comparing Eqs. (11.15) and (11.16), we conclude that:

$${S}_{f}A = A\circ {m}_{f}\ {e}^{\theta \circ {a}_{f}^{-1}{L}_{y}}$$ (11.17)

We now apply Eq. (11.17), on the vector ${\vec e}_2$ using the Einstein summation convention on repeated indices:

$${\left.{{S}_{f}A{\vec{e}}_{2}}\right\vert}_{a} = {\left.{A\circ {m}_{f}\ {e}^{\theta \circ {a}_{f}^{-1}{L}_{y}}{\vec{e}}_{2}}\right\vert}_{a}$$

$${S}_{f;ab}{A}_{b2} = {A}_{a2}\circ {m}_{f}$$

$${\rm b}{\rm e}{\rm c}{\rm a}{\rm u}{\rm s}{\rm e}\ {e}^{\theta \circ {a}_{f}^{-1}{L}_{y}}{\vec{e}}_{2} = {\vec{e}}_{2}\ {\rm i}.{\rm e}.,~{\rm n}{\rm o}{\rm r}{\rm m}{\rm a}{\rm l}~{\rm f}{\rm o}{\rm r}{\rm m}!$$ (11.18)

Therefore, we deduce from the Eq. (11.18) that the vector $\vec n$ defined as $A{\vec e}_2$ transforms as follows:

$${S}_{f}\vec{n} = \vec{n}\circ {m}_{f}$$ (11.19)

Equation (11.19) indicates that $\vec n$ is truly an invariant vector function of phase space as well as being a solution of the spin motion. In other words it transforms under the action $S_f$ as an orbital function would. Of course it was designed to be so by virtue of the assumed existence of the normal form.