Electron Screened Single Scattering and NIEL

The present treatment [eal12] of electron–nucleus interaction is based on numerical and analytical approximations of the Mott differential cross section. It accounts for effects due to screened Coulomb potentials, finite sizes and finite rest masses of nuclei for electron with kinetic energies above 200 keV and up to ultra high. This treatment allows one to determine both the total and differential cross sections, thus, to calculate the resulting nuclear and non-ionizing stopping powers (NIEL). Above a few hundreds of MeV, neglecting the effects of finite sizes and rest masses of recoil nuclei the stopping power and NIEL result to be largely underestimated, while, above a few tens of MeV prevents a further large increase, thus, resulting in approaching almost constant values at high energies.

The non-ionizing energy loss (NIEL) is the energy lost from a particle traversing a unit length of a medium through physical process resulting in permanent displacement damages (e.g. see Ref.[LR07]). The nuclear stopping power and NIEL deposition due to elastic Coulomb scatterings from protons and light and heavy ions traversing an absorber were previously described [eal11] and are available in Geant4 (Single Scattering, Screened Coulomb Potential and NIEL) (see also Sections 1.6, 1.6.1, 2.1.4–2.1.4.2, 4.2.1.6 of Ref. [LR11]). In the present model included in Geant4, the nuclear stopping power and NIEL deposition due to elastic Coulomb scatterings of electrons are treated up to ultra relativistic energies.

Scattering Cross Section of Electrons on Nuclei

The scattering of electrons by unscreened atomic nuclei was treated by Mott extending a method of Wentzel dealing with incident and scattered waves on point-like nuclei and including effects related to the spin of electrons. The differential cross section (DCS), denoted the Mott differential cross section (MDCS), was expressed by Mott as two conditionally convergent infinite series in terms of Legendre expansions. In Mott–Wentzel treatment, the scattering occurs on a field of force generating a radially dependent Coulomb, unscreened (screened) in Mott (Wentzel), potential. Furthermore, the MDCS was derived in the laboratory reference system for infinitely heavy nuclei initially at rest with negligible spin effects and must be numerically evaluated for any specific nuclear target. Effects related to the recoil and finite rest mass of the target nucleus (\(M\)) were neglected. Thus, in this framework the total energy of electrons has to be smaller or much smaller than \(M c^2\).

The MDCS is usually expressed as:

(82)\[\frac{d\sigma^{\rm Mott}(\theta)}{d\Omega} = \frac{d\sigma^{\rm Rut}}{d\Omega} \,\, \mathcal{R}^{\rm Mott},\]

where \(\mathcal{R}^{\rm Mott}\) is the ratio between the MDCS and Rutherford’s formula (RDCS, see Equation (1) of Ref. [eal12]). For electrons with kinetic energies from several keV up to 900 MeV and target nuclei with \(1 \leqslant Z \leqslant 90\), Lijian et al. [LQZ95] provided a practical interpolated expression (Eq.(92)) for \(\mathcal{R}^{\rm Mott}\) with an average error less than 1%; in the present treatment, that expression (Interpolated Expression for ) is the one assumed for \(\mathcal{R}^{\rm Mott}\) in Eq.(82) hereafter. The analytical expression derived by McKinley and Feshbach [MF48] for the ratio with respect to Rutherford’s formula (Eq.(7) of Ref. [MF48]) is given by:

(83)\[\mathcal{R}^{\rm McF} = 1-\beta^2\sin^2\!\left(\theta/2\right) +Z\,\alpha\beta\pi \sin\!\left(\theta/2\right)\left[1- \sin\!\left(\theta/2\right)\right]\]

with the corresponding differential cross section (McFDCS)

(84)\[\frac{d\sigma^{\rm McF}}{d\Omega} = \frac{d\sigma^{\rm Rut}}{d\Omega} \,\,\mathcal{R}^{\rm McF}.\]

Furthermore, for \(M c^2\) much larger than the total energy of incoming electron energies the distinction between laboratory (i.e., the system in which the target particle is initially at rest) and center-of-mass (CoM) systems disappears (e.g., see discussion in Section 1.6.1 of Ref. [LR11]). Furthermore, in the CoM of the reaction the energy transferred from an electron to a nucleus initially at rest in the laboratory system (i.e., its recoil kinetic energy \(T\)) is related with the maximum energy transferable \(T_{\rm max}\) as

(85)\[T = T_{\rm max} \,\sin^2 (\theta'/2)\]

(e.g., see Eqs. (1.27, 1.95) at page 11 and 31, respectively, of Ref. [LR11]), where \(\theta'\) is the scattering angle in the CoM system. In addition, one obtains

(86)\[dT = \frac{ T_{\rm max}}{4 \pi} \, d\Omega' .\]

Since for \(Mc^2\) much larger than the electron energy, \(\theta\) \(\approx \theta'\), one finds that Eq.(85) can be approximated as

(87)\[T \simeq T_{\rm max} \sin^2 \left(\theta/2\right),\]

(88)\[\Longrightarrow \sin^2 \left(\theta/2\right) = \frac{T}{ T_{\rm max}}\]

and

(89)\[dT \simeq \frac{ T_{\rm max}}{4 \pi} \, d\Omega .\]

Using Eqs.(83), (88), (89), Rutherford’s formula and Eq.(84) can be respectively rewritten as:

(90)\[\begin{split}\Longrightarrow \frac{d\sigma^{\rm Rut}}{dT} &= \left(\! \frac{Ze^2}{ p \beta c}\!\right)^2\frac{ \pi T_{\rm max}}{T^2},\\ \Longrightarrow \frac{d\sigma^{\rm McF}}{T} \! & = \!\! \left(\! \frac{Ze^2}{ p \beta c}\!\right)^2\!\frac{ \pi T_{\rm max}}{T^2} \!\! \left[1\!-\!\beta \frac{T}{ T_{\rm max}}\! \left( \beta\! + \! Z\alpha\pi \right)\! + \!Z\alpha\beta\pi \! \sqrt{\frac{T}{ T_{\rm max}}} \right]\!\\ & = \!\! \left(\! \frac{Ze^2}{ p \beta c}\!\right)^2\!\frac{ \pi T_{\rm max}}{T^2} \,\, \mathcal{R}^{\rm McF}(T)\end{split}\]

with

(91)\[\mathcal{R}^{\rm McF}(T) = \left[1\!-\!\beta \frac{T}{ T_{\rm max}}\! \left( \beta\! + \! Z\alpha\pi \right)\! + \!Z\alpha\beta\pi \! \sqrt{\frac{T}{ T_{\rm max}}} \right].\]

Finally, in a similar way the MDCS (Eq.(82)) is

\[\begin{split}\frac{d\sigma^{\rm Mott}(T)}{dT} &= \frac{d\sigma^{\rm Rut}}{dT} \,\, \mathcal{R}^{\rm Mott}(T)\\ &= \left(\! \frac{Ze^2}{ p \beta c}\!\right)^2\!\frac{ \pi T_{\rm max}}{T^2} \,\, \mathcal{R}^{\rm Mott}(T)\end{split}\]

with \(\mathcal{R}^{\rm Mott} (T)\) from Eq.(94).

Interpolated Expression for \(\mathcal{R}^{\rm Mott}\)

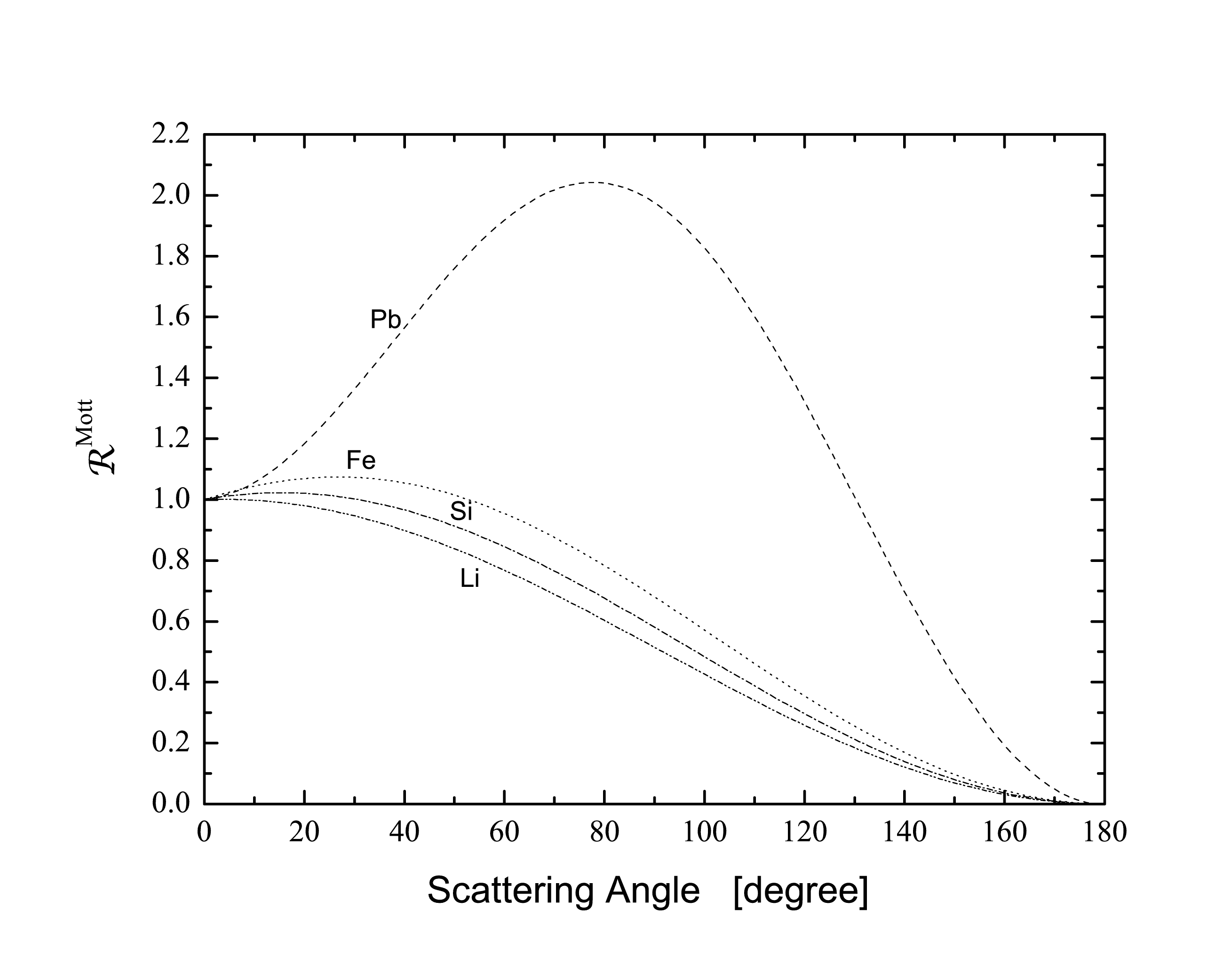
Fig. 21 \(\mathcal{R}^{\rm Mott}\) obtained from Eq.(92) at 100 MeV for Li, Si, Fe and Pb nuclei as a function of scattering angle.

Recently, Lijian, Quing and Zhengming [LQZ95] provided a practical interpolated expression (Eq.(92)) which is a function of both \(\theta\) and \(\beta\) for electron energies from several keV up to 900 MeV, i.e.,

(92)\[\mathcal{R}^{\rm Mott} = \sum_{\textrm{j}=0}^4 a_\textrm{j}(Z,\beta)(1-\cos\theta)^{\textrm{j}/2},\]

where

(93)\[a_\textrm{j}(Z,\beta)=\sum_{\textrm{k}=1}^6 b_\textrm{k,j}(Z)(\beta-\overline{\beta})^{\textrm{k}-1},\]

and \(\overline{\beta}\,c=0.7181287 \,c\) is the mean velocity of electrons within the above mentioned energy range. The coefficients \(b_\textrm{k,j}(Z)\) are listed in Table 1 of Ref. [LQZ95] for \(1 \leqslant Z \leqslant 90\). Boschini et al. (2013) [eal13] provided an extended numerical solution for the Mott differential cross section on nuclei up to \(Z=118\) for both electrons and positrons. \(\mathcal{R}^{\rm Mott}\) obtained from Eq.(92) at 100 MeV is shown in Fig. 21 for Li, Si, Fe and Pb nuclei as a function of scattering angle. Furthermore, it has to be remarked that the energy dependence of \(\mathcal{R}^{\rm Mott}\) from Eq.(92) was studied and observed to be negligible above \(\approx 10\,\)MeV (for instance, see Eq.(93)).

Finally, from Eqs.(85), (92) (see also Equation (1.93) at page 31 of Ref.[LR11]), one finds that \(\mathcal{R}^{\rm Mott}\) can be expressed in terms of the transferred energy \(T\) as

(94)\[ \mathcal{R}^{\rm Mott} (T)= \sum_{\textrm{j}=0}^4 a_\textrm{j}(Z,\beta)\left(\frac{2T}{T_{\rm max}}\right)^{\textrm{j}/2}.\]

Screened Coulomb Potentials

The simple scattering model due to Wentzel with a single exponential screening function (see Eq. (2.71) of Ref. [LR11]) was repeatedly employed in treating single and multiple Coulomb scattering with screened potentials. Neglecting effects like those related to spin and finite size of nuclei, for proton and nucleus interactions on nuclei it was shown that the resulting elastic differential cross section of a projectile with bare nuclear-charge \(ez\) on a target with bare nuclear-charge \(eZ\) differs from the Rutherford differential cross section (RDCS) by an additional term, the screening parameter, which prevents the divergence of the cross section when the angle \(\theta\) of scattered particles approaches \(0^\circ\) (see Section 1.6.1 of Ref. [LR11]). For \(z=1\) particles the screening parameter \(A_{\rm s,M}\) is expressed as

(95)\[A_{\rm s,M}=\left(\frac{\hbar}{2\,p\ a_{\rm TF}}\right)^2\left[1.13+3.76 \times \left(\frac{\alpha Z}{\beta}\right)^2\right]\]

where \(\alpha\), \(c\) and \(\hbar\) are the fine-structure constant, speed of light and reduced Planck constant, respectively; \(p\) (\(\beta c\)) is the momentum (velocity) of the incoming particle undergoing the scattering onto a target supposed to be initially at rest, i.e., in the laboratory system; \(a_{\rm TF}\) is the screening length suggested by Thomas–Fermi

\[{\rm {a_{TF}}}=\frac{C_{\rm TF} \,{\rm {a_{0}}} }{Z^{1/3}}\]

with

\[{\rm {a_{0}}} =\frac{\hbar^2}{m e^2}\]

the Bohr radius, \(m\) the electron rest mass and

\[C_{\rm TF} = \frac{1}{2}\left(\frac{3 \, \pi}{4} \right)^{2/3} \simeq 0.88534\]

a constant introduced in the Thomas–Fermi model (see Ref. [eal11], Eq.(2.73, 2,82) of Ref. [LR11], and references therein). The modified Rutherford’s formula \({d\sigma^{\rm WM}(\theta)}/{d\Omega}\), i.e., the differential cross section obtained from the Wentzel–Molière treatment of the single scattering on screened nuclear potential is given by (see Eq.(2.84) of Ref. [LR11] and Ref. [eal11], and references therein):

(96)\[\begin{split}\frac{d\sigma^{\rm WM}(\theta)}{d\Omega} &= \left(\frac{zZe^2}{2\,p \, \beta c }\right)^2\frac{1}{\left[A_{\rm s,M}+\sin^2({\theta}/2)\right]^2} \\ &= \frac{d\sigma^{\rm Rut}}{d\Omega} \,\,\mathfrak{F}^2(\theta) .\end{split}\]

with

(97)\[\mathfrak{F}(\theta) = \frac{\sin^2(\theta/2)}{A_{\rm s,M}+\sin^2({\theta}/2)}.\]

\(\mathfrak{F}(\theta)\), the screening factor, depends on the scattering angle \(\theta\) and the screening parameter \(A_{\rm s,M}\). As discussed in Finite Rest Mass of Target Nucleus, the term \(A_{\rm s,M}\) (the screening parameter) cannot be neglected in the DCS (Eq.(96)) for scattering angles (\(\theta\)) within a forward (with respect to the electron direction) angular region narrowing with increasing energy from several degrees (for high-Z material) at 200 keV down to less than or much less than a mrad above 200 MeV.

An approximated description of elastic interactions of electrons with screened Coulomb fields of nuclei can be obtained by the factorization of the MDCS, i.e., involving Rutherford’s formula \({d\sigma^{\rm Rut}}/{d\Omega}\) for particle with \(z=1\), the screening factor \(\mathfrak{F}(\theta)\) and the ratio \(\mathcal{R}^{\rm Mott}\) between the RDCS and MDCS:

(98)\[ \frac{d\sigma^{\rm Mott}_{\rm sc}(\theta)}{d\Omega} \simeq \frac{d\sigma^{\rm Rut}}{d\Omega} \,\, \mathfrak{F}^2(\theta)\,\, \mathcal{R}^{\rm Mott}.\]

Thus, the corresponding screened differential cross section derived using the analytical expression from McKinley and Feshbach [MF48] can be approximated with

(99)\[ \frac{d\sigma^{\rm McF}_{\rm sc}(\theta)}{d\Omega} \simeq \frac{d\sigma^{\rm Rut}}{d\Omega} \,\, \mathfrak{F}^2(\theta)\,\, \mathcal{R}^{\rm McF}.\]

Zeitler and Olsen [ZO64] suggested that for electron energies above 200 keV the overlap of spin and screening effects is small for all elements and for all energies; for lower energies the overlapping of the spin and screening effects may be appreciable for heavy elements and large angles.

Finite Nuclear Size

The ratio between the actual measured and that expected from the point-like differential cross section expresses the square of nuclear form factor \(\left|F \right|\) which, in turn, depends on the momentum transfer \(q\), i.e., that acquired by the target initially at rest:

(100)\[q=\frac{\sqrt{T(T+2Mc^2)}}{c},\]

with \(T\) from Eq.(85) or for \(Mc^2\) larger or much larger than the electron energy from its approximate expression Eq.(87).

The approximated (factorized) differential cross section for elastic interactions of electrons with screened Coulomb fields of nuclei (Eq.(98)) accounting for the effects due to the finite nuclear size is given by:

(101)\[\frac{d\sigma^{\rm Mott}_{{\rm sc},F}(\theta)}{d\Omega} \simeq \frac{d\sigma^{\rm Rut}}{d\Omega} \,\, \mathfrak{F}^2(\theta)\,\, \mathcal{R}^{\rm Mott} \left|F (q)\right| ^2.\]

Thus, using the analytical expression derived by [MF48] (Eq.(83)) one obtains that the corresponding screened differential cross section (Eq.(99)) accounting for the finite nuclear size effects

(102)\[\begin{split}\frac{d\sigma^{\rm McF}_{{\rm sc},F}(\theta)}{d\Omega} & \simeq \frac{d\sigma^{\rm Rut}}{d\Omega} \,\, \mathfrak{F}^2(\theta)\,\, \mathcal{R}^{\rm McF} \left|F (q)\right| ^2\\ & = \frac{d\sigma^{\rm Rut}}{d\Omega} \,\, \mathfrak{F}^2(\theta) \left|F (q)\right| ^2\\ & \times \left\{1\!-\!\beta^2\sin^2\!\left(\theta/2\right) +Z\,\alpha\beta\pi \sin\!\left(\theta/2\right)\left[1- \sin\!\left(\theta/2\right)\right]\right\} .\end{split}\]

In terms of kinetic energy, one can respectively rewrite Eqs.(101), (102) as

(103)\[\begin{split}\frac{d\sigma^{\rm Mott}_{{\rm sc},F}(T)}{dT} &= \frac{d\sigma^{\rm Rut}}{dT} \,\,\mathfrak{F}^2(T) \,\,\mathcal{R}^{\rm Mott}(T)\,\,\left|F (q)\right| ^2 \\ \frac{d\sigma^{\rm McF}_{{\rm sc},F}(T)}{dT} &\simeq \frac{d\sigma^{\rm Rut}(T)}{dT} \,\, \mathfrak{F}^2(T)\,\,\, \mathcal{R}^{\rm McF} (T)\,\, \left|F (q)\right| ^2\end{split}\]

with \({d\sigma^{\rm Rut}}/{dT}\) from Eq.(90), \(\mathcal{R}^{\rm Mott}(T)\) from Eq.(94), \(\mathcal{R}^{\rm McF} (T)\) from Eq.(91) and, using Eqs.(85), (87), (97),

\[\mathfrak{F}(T)= \frac{T}{ T_{\rm max} A_{\rm s,M}+T}.\]

For instance, the form factor \(F_{\rm exp}\) is

(104)\[F_{\rm exp}(q)=\left[1+ \frac{1}{12}\left(\frac{q r_{\rm n}}{\hbar}\right)^2\right]^{-2},\]

where \(r_{\rm n}\) is the nuclear radius, \(r_{\rm n}\) can be parameterized by

(105)\[r_{\rm n}= 1.27 A^{0.27}~ \textrm{fm}\]

with \(A\) the atomic weight. Equation (105) provides values of \(r_{\rm n}\) in agreement up to heavy nuclei (like Pb and U) with those available, for instance, in Table 1 of Ref. [VJV87].

Finite Rest Mass of Target Nucleus

The DCS treated in Scattering Cross Section of Electrons on Nuclei to Finite Nuclear Size is based on the extension of MDCS to include effects due to interactions on screened Coulomb potentials of nuclei and their finite size. However, the electron energies were considered small (or much smaller) with respect to that (\(M c^2\)) corresponding to rest mass (\(M\)) target nuclei.

The Rutherford scattering on screened Coulomb fields, i.e., under the action of a central forces, by massive charged particles at energies large or much larger than \(M c^2\) was treated by Boschini et al. [eal11] in the CoM system (see also Sections 1.6, 1.6.1, 2.1.4.2 of Ref. [LR11] and references therein). It was shown that the differential cross section (\(d\sigma^{\rm WM}(\theta')/d\Omega'\) with \(\theta'\) the scattering angle in the CoM system) is that one derived for describing the interaction on a fixed scattering center of a particle with

• momentum \(p_{\rm r}'\) equal to the momentum of the incoming particle (i.e., the electron in the present treatment) in the CoM system

• rest mass equal to the relativistic reduced mass \(\mu_{\rm rel}\) (see Eqs.(1.80, 1.81) in Ref. [LR11]).

\(\mu_{\rm rel}\) is given by

\[\begin{split}\mu_{\rm rel} &= \frac{m M }{M_{1,2}}\\ &= \frac{m M c}{\sqrt{m^2 c^2 + M^2 c^2 + 2\,M \sqrt{m^2 c^4 + p^2 c^2}}} ,\end{split}\]

where \(p\) is the momentum of the incoming particle (the electron in the present treatment) in the laboratory system; \(m\) is the rest mass of the incoming particle (i.e., the electron rest mass); \(M_{1,2}\) is the invariant mass (Section 1.3.2 of Ref. [LR11] of the two-particle system. Thus, the velocity of the interacting particle is (see Eq.(1.82) at of Ref. [LR11])

\[\beta_{\rm r}' c = c \sqrt{\left[1+ \left(\frac{\mu_{\rm rel} c}{p_{\rm r}' } \right)^2 \right]^{-1}}.\]

For an incoming particle with \(z=1\), \(d\sigma^{\rm WM}(\theta')/d\Omega'\) is given by

(106)\[\frac{d\sigma^{\rm WM'}(\theta')}{d\Omega'} = \left(\frac{Ze^2}{2\,p_{\rm r}' \, \beta_{\rm r}' c }\right)^2 \frac{1}{\left[A_{\rm s}+\sin^2({\theta'}/2)\right]^2},\]

with

(107)\[A_{\rm s}=\left(\frac{\hbar}{2\,p_{\rm r}'\, a_{\rm TF}}\right)^2 \left[1.13+3.76 \times \left(\frac{\alpha Z}{\beta_{\rm r}'}\right)^2\right]\]

the screening factor (see Eqs.(2.87, 2.88) of Ref. [LR11]). Eq.(106) can be rewritten as

(108)\[\frac{d\sigma^{\rm WM'}(\theta')}{d\Omega'} = \frac{d\sigma^{\rm Rut'}(\theta')}{d\Omega'} \,\, \mathfrak{F}_{\rm CoM}^2(\theta')\]

with

(109)\[\frac{d\sigma^{\rm Rut'}(\theta')}{d\Omega'} = \left(\! \frac{Ze^2}{2 p_{\rm r}' \beta_{\rm r}' c }\right)^2 \frac{1}{ \sin^4(\theta'/2)}\]

the corresponding RDCS for the reaction in the CoM system (see Eq.(1.79) of Ref. [LR11]] and

(110)\[\mathfrak{F}_{\rm CoM}(\theta') = \frac{\sin^2(\theta'/2)}{A_{\rm s}+\sin^2({\theta'}/2)}\]

the screening factor. Using Eqs.(85) and (86), one can respectively rewrite Eqs.(109), (110), (108), (106) as

(111)\[\frac{d\sigma^{\rm Rut'}}{dT} =\pi \left(\! \frac{Ze^2}{ p_{\rm r}' \beta_{\rm r}' c }\right)^2 \frac{T_{\rm max}}{ T^2}\]

(112)\[\mathfrak{F}_{\rm CoM}(T) = \frac{T}{ T_{\rm max}A_{\rm s}+T}\]

\[\frac{d\sigma^{\rm WM'}(T)}{dT} = \frac{d\sigma^{\rm Rut'}}{dT} \,\,\mathfrak{F}_{\rm CoM}(T)\]

\[\frac{d\sigma^{\rm WM'}(T)}{dT} = \pi \left(\! \frac{Ze^2}{ p_{\rm r}' \beta_{\rm r}' c }\right)^2 \frac{T_{\rm max}}{ \left( T_{\rm max}A_{\rm s}+T\right)^2} .\]

(see Eq.(2.90) of Ref.[LR11] or Eq.(13) of Ref.[eal11]).

To account for the finite rest mass of target nucleus the factorized MDCS (Eq.(101)) has to be re-expressed in the CoM system using as:

(113)\[\frac{d\sigma^{\rm Mott}_{{\rm sc},F,\rm CoM}(\theta')}{d\Omega'} \!\! \simeq \!\!\frac{d\sigma^{\rm Rut'}(\theta')}{d\Omega'} \,\, \mathfrak{F}_{\rm CoM}^2(\theta')\,\, \mathcal{R}^{\rm Mott}_{\rm CoM}(\theta')\,\,\left|F (q)\right| ^2 \!,\]

where \(F (q)\) is the nuclear form factor (Finite Nuclear Size) with \(q\), the momentum transfer to the recoil nucleus (Eq.(100)); finally, as discussed in Interpolated Expression for , \(\mathcal{R}^{\rm Mott}\) exhibits almost no dependence on electron energy above \(\approx 10\,\)MeV, thus, since at low energies \(\theta \backsimeq \theta'\) and \(\beta \backsimeq \beta_{\rm r}'\), \(\mathcal{R}^{\rm Mott}_{\rm CoM}(\theta')\) is obtained replacing \(\theta\) and \(\beta_{\rm r}'\) with \(\theta'\) and \(\beta_{\rm r}'\), respectively, in Eq.(92).

Using the analytical expression derived by McKinley and Feshbach [MF48], one finds that the corresponding screened differential cross section accounting for the finite nuclear size effects (Eqs.(102)) can be re-expressed as

(114)\[\begin{split}\frac{d\sigma^{\rm McF}_{{\rm sc},F, \rm CoM}(\theta')}{d\Omega'} \simeq \frac{d\sigma^{\rm Rut'}(\theta')}{d\Omega'} \,\, \mathfrak{F}_{\rm CoM}^2(\theta')\,\,\, \mathcal{R}_{\rm CoM}^{\rm McF} (\theta')\,\, \left|F (q)\right| ^2\\\end{split}\]

with

(115)\[\mathcal{R}^{\rm McF}_{\rm CoM} (\theta') = \left\{\!1\!-\!\beta_{\rm r}^2\sin^2\!\left(\theta'/2\right) \!+\!Z\,\alpha\beta_{\rm r}'\pi \sin\!\left(\theta'/2\right)\left[1\!- \!\sin\!\left(\theta'/2\right)\right]\!\right\} .\]

In terms of kinetic energy \(T\), from Eqs.(85) and (86), one can respectively rewrite Eqs.(113) and (114) as

(116)\[\frac{d\sigma^{\rm Mott}_{{\rm sc},F,\rm CoM}(T)}{dT} = \frac{d\sigma^{\rm Rut'}}{dT} \,\,\mathfrak{F}_{\rm CoM}^2(T) \,\,\mathcal{R}^{\rm Mott}_{\rm CoM}(T)\,\,\left|F (q)\right| ^2\]

(117)\[\frac{d\sigma^{\rm McF}_{{\rm sc},F, \rm CoM}(T)}{dT} \simeq \frac{d\sigma^{\rm Rut'}(T)}{dT} \,\, \mathfrak{F}_{\rm CoM}^2(T)\,\,\, \mathcal{R}_{\rm CoM}^{\rm McF} (T)\,\, \left|F (q)\right| ^2\]

with \({d\sigma^{\rm Rut'}}/{dT}\) from Eq.(111), \(\mathfrak{F}_{\rm CoM}(T)\) from Eq.(112) and \(\mathcal{R}^{\rm McF}_{\rm CoM}(T)\) replacing \(\beta\) with \(\beta_{\rm r}'\) in Eq.(91), i.e.,

\[\mathcal{R}^{\rm McF}_{\rm CoM}(T)= \left[1\!-\!\beta_{\rm r}'\frac{T}{ T_{\rm max}}\! \left( \beta_{\rm r}'\! + \! Z\alpha\pi \right)\! + \!Z\alpha\beta_{\rm r}'\pi \! \sqrt{\frac{T}{ T_{\rm max}}} \right].\]

Finally, as discussed in Interpolated Expression for , \(\mathcal{R}^{\rm Mott}(T)\) exhibits almost no dependence on electron energy above \(\approx 10\,\)MeV, thus, since at low energies \(\theta \backsimeq \theta'\) and \(\beta \backsimeq \beta_{\rm r}'\), \(\mathcal{R}^{\rm Mott}_{\rm CoM}(T)\) is obtained replacing \(\beta\) with \(\beta_{\rm r}'\) in Eq.(94).

Nuclear Stopping Power of Electrons

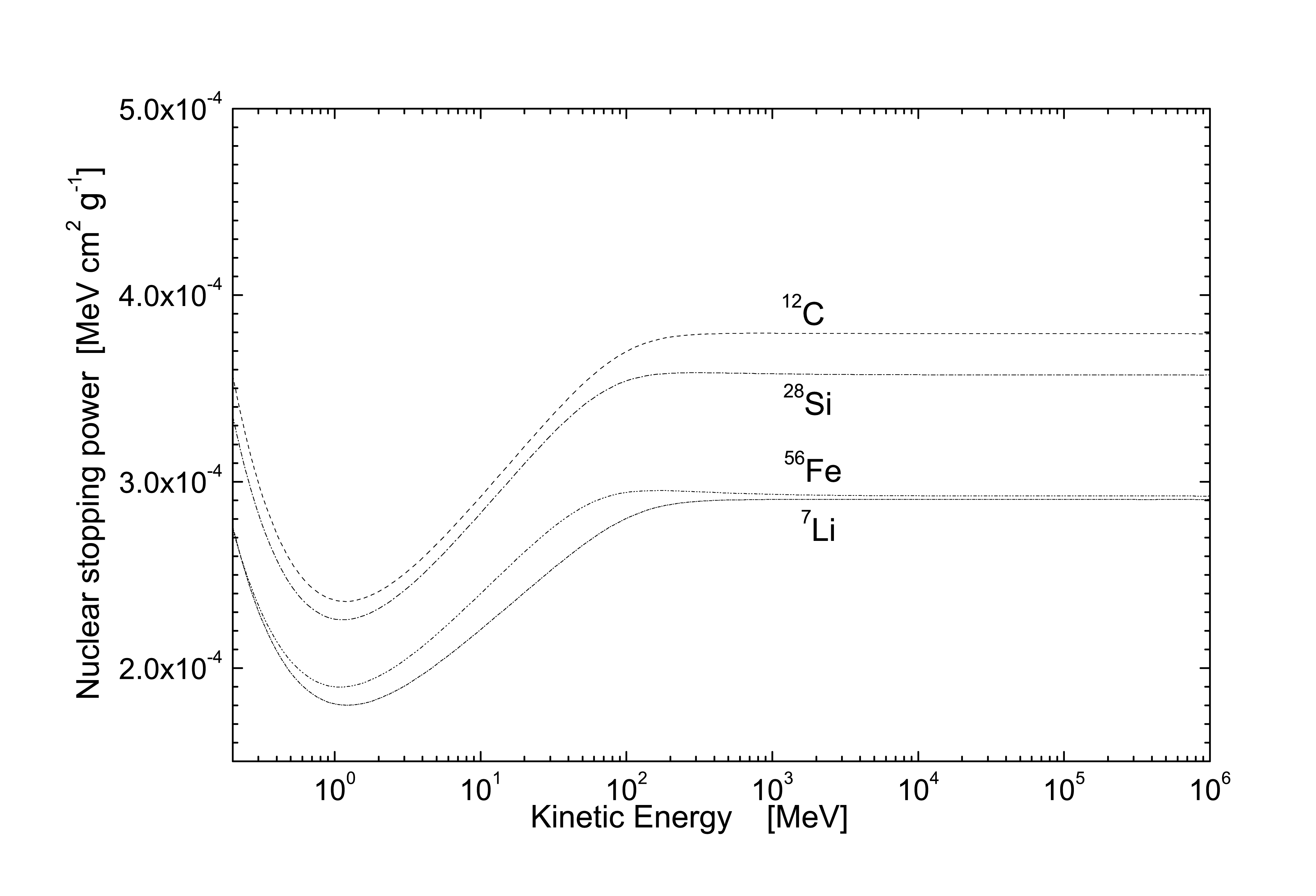
Fig. 22 In MeVcm²/g, nuclear stopping powers in ⁷Li, ¹²C, ²⁸Si and ⁵⁶Fe calculated from Eq.(119) and divided by the density of the material as a function of the kinetic energy of electrons from 200 keV up to 1 TeV.

Using Eq.(116), the nuclear stopping power in MeV cm^-1 of Coulomb electron–nucleus interaction can be obtained as

(118)\[- \left(\frac{dE}{dx}\right)_{\rm nucl}^{\rm Mott} = {n_A}\int_{0}^{T_{max}} \frac{d\sigma^{\rm Mott}_{{\rm sc},F,\rm CoM}(T)}{dT} \, T \,d T\]

with \(n_A\) the number of nuclei (atoms) per unit of volume (see Eq.(1.71) of Ref. [LR11]) and, finally, the negative sign indicates that the energy is lost by the electron (thus, achieved by recoil targets). Using the analytical approximation derived by McKinley and Feshbach [MF48], i.e., Eq.(117), for the nuclear stopping power one finds

(119)\[- \left(\frac{dE}{dx}\right)_{\rm nucl}^{\rm McF} = {n_A}\int_{0}^{T_{max}} \frac{d\sigma^{\rm McF}_{{\rm sc},F,\rm CoM}(T)}{dT} \, T \,d T.\]

As already mentioned in Finite Rest Mass of Target Nucleus, the large momentum transfers corresponding to large scattering angles are disfavored by effects due to the finite nuclear size accounted for by means of the nuclear form factor (Finite Nuclear Size). For instance, the ratios of nuclear stopping powers of electrons in silicon are shown in Ref. [eal12] as a function of the kinetic energies of electrons from 200 keV up to 1 TeV. These ratios are the nuclear stopping powers calculated neglecting

• nuclear size effects (i.e., for \(\left|F_{\rm exp}\right|^2=1\))

• effects due to the finite rest mass of the target nucleus (i.e., in Eq.(119) replacing \({d\sigma^{\rm McF}_{{\rm sc},F,\rm CoM}(T)}/{dT}\) with \({d\sigma^{\rm McF}_{{\rm sc},F}(T)}/{dT}\) from Eq. (103) both divided by that one obtained using Eq.(119).

Above a few tens of MeV, a larger stopping power is found assuming \(\left|F_{\rm exp}\right|^2=1\) and, in addition, above a few hundreds of MeV the stopping power largely decreases when the effects of nuclear rest mass are not accounted for.

In Fig. 22, the nuclear stopping powers in ⁷Li, ¹²C, ²⁸Si and ⁵⁶Fe are shown as a function of the kinetic energy of electrons from 200 keV up to 1 TeV. These nuclear stopping powers are calculated from Eq.(119) and divided by the density of the medium.

Non-Ionizing Energy-Loss of Electrons

In case of Coulomb scattering of electrons on nuclei, the non-ionizing energy loss can be calculated using (as discussed in Scattering Cross Section of Electrons on Nuclei to Nuclear Stopping Power of Electrons) the MDCRS or its approximate expression McFDCS (e.g., Eqs.(116), (117), respectively), once the screened Coulomb fields, finite sizes and rest masses of nuclei are accounted for, i.e., in MeV/cm

(120)\[- \left(\frac{dE}{dx}\right)_{\rm n,Mott}^{\rm NIEL} = n_A\,\int^{T_{max}}_{T_d} \!T\,L(T)\,\frac{d\sigma^{\rm Mott}_{{\rm sc},F,\rm CoM}(T)}{dT}\,dT\]

or

(121)\[- \left(\frac{dE}{dx}\right)_{\rm n,McF}^{\rm NIEL} = n_A\,\int^{T_{max}}_{T_d} \!T\,L(T)\,\frac{d\sigma^{\rm McF}_{{\rm sc},F,\rm CoM}(T)}{dT}\,dT\]

(see Eq.(4.113) and Sections 4.2.1–4.2.1.2 of Ref. [LR11]), where \(T\) is the kinetic energy transferred to the target nucleus, \(L(T)\) is the fraction of \(T\) deposited by means of displacement processes. The Lindhard partition function, \(L(T)\), can be approximated using the Norgett–Robintson–Torrens expression (see Eqs.(4.121, 4.123) of Ref. [LR11] and references therein).  \(T_{\rm de}= T\, L(T)\) is the damage energy, i.e., the energy deposited by a recoil nucleus with kinetic energy \(T\) via displacement damages inside the medium. In Eqs.(120) and (121), the integral is computed from the minimum energy \(T_d\), the threshold energy for displacement, i.e., that energy necessary to displace the atom from its lattice position up to the maximum energy \(T_{max}\) that can be transferred during a single collision process. For instance, \(T_d\) is about 21 eV in silicon requiring electrons with kinetic energies above \(\approx 220\,\)keV. As already discussed with respect to nuclear stopping powers in Nuclear Stopping Power of Electrons, the large momentum transfers (corresponding to large scattering angles) are disfavored by effects due to the finite nuclear size accounted for by the nuclear form factor. For instance, the ratios of NIELs for electrons in silicon are shown in Ref. [eal12] as a function of the kinetic energy of electrons from 220 keV up to 1 TeV. These ratios are the NIELs calculated neglecting

• nuclear size effects (i.e., for \(\left|F_{\rm exp}\right|^2=1\))

• effects due to the finite rest mass of the target nucleus (i.e., in Eq.(121) replacing \({d\sigma^{\rm McF}_{{\rm sc},F,\rm CoM}(T)}/{dT}\) with \({d\sigma^{\rm McF}_{{\rm sc},F}(T)}/{dT}\) from Eq.` (103) both divided by that one obtained using Eq.(121).

Above ~ 10 MeV, the NIEL is ~20% larger assuming \(\left|F_{\rm exp}\right|^2=1\) and, in addition, above 100–200 MeV the calculated NIEL largely decreases when the effects of nuclear rest mass are not accounted for.

G4eSingleScatteringModel

The G4eSingleScatteringModel performs the single scattering interaction of electrons on nuclei. The differential cross section (DCS) for the energy transferred is define in the G4ScreeningMottCrossSection class. In this class the M.Boschini’s et al. [eal13] Mott differential cross Section approximation is implemented. This CDS is modified by the introduction of the Moliere’s [Moliere48] screening coefficient. In addition the exponential charge distribution Nuclear Form Factor is applied [BKMM02]. This treatment is fully performed in the center of mass system and the usual Lorentz transformations are applied to obtained the energy and momentum quantities in the laboratory system after scattering. This model well simulates the interacting process for low scattering angles and it is suitable for high energy electrons (from 200 keV) incident on medium light target nuclei. The nuclear energy loss (i.e. nuclear stopping power) is calculated for every single interaction. In addition the production of secondary scattered nuclei is simulated from a threshold kinetic energy which can be decided by the user (threshold energy for displacement).

The method

In the G4eSingleScatteringModel the method ComputeCrossSectionPerAtom() performs the total cross section computation. The SetupParticle() and the DefineMaterial() methods are called to defined the incident and target particles. Before the total cross section computation, the SetupKinematic() method of the G4ScreeningMottCrossSection class calculates all the physical quantities in the center of mass system (CM). The scattering in the CM system is equivalent to the one of an effective particle which interacts with a fixed scattering center. The effective particle rest mass is equal to the relativistic reduced mass of the system \(\mu\) whose expression is calculated by:

\[\mu = m\frac{Mc^2}{E_{cm}}\]

where \(m\) and \(M\) are rest masses of the electron and of the target nuclei respectively. \(E_{cm}\) is the total center of mass energy and, since the target is at rest before scattering, its expression is calculated by:

\[E_{cm}=\sqrt{(mc^2)^2+(Mc^2)^2+2E' Mc^2}\]

where \(E =\gamma' mc^2\) is the total energy of the electron before scattering in the laboratory system. The momentum and the scattering angle of the effective particle are equal to the corresponding quantities calculated in the center of mass system (\(p\equiv p_{cm}\), \(\theta\equiv \theta_{cm}\)) of the incident electron:

\[pc=p'c\frac{Mc^2}{E_{cm}}\]

where \(p'\) is the momentum of the incident electron calculated in the laboratory system. The velocity of the effective particle is related with its momentum by the following expression:

\[\frac{1}{\beta^2}= 1+\Big(\frac{\mu c^2}{pc}\Big)^2\]

The integration of the DCS is performed by the NuclearCrossSection() method of the G4ScreeningMottCrossSection:

\[\sigma_{tot}=2\pi\int_{\theta_{min}}^{\theta_{max}} \frac{d\sigma(\theta)}{{d\Omega}}\sin\theta d\theta\]

The integration is performed in the scattering range [0 ;\(\pi\)] but the user can decide to vary the minimum (\(\theta_{min}\)) and the maximum (\(\theta_{max}\)) scattering angles. The DCS is then given by:

\[\frac{d\sigma(\theta)}{{d\Omega}}=\Bigg(\frac{Ze^2}{\mu c^2\ \beta^2 \gamma}\Bigg)^2 \frac{R_{McF}|F_N(q)|^2}{\big(2A_s+2\sin^2(\theta/2)\big)^2}\]

where \(Z\) is the atomic number of the nucleus, \(A_s\) is the screening coefficient whose expression has been given by Moliere [Moliere48] :

(122)\[A_s=\bigg(\frac{\hbar}{2p\ a_{TF}}\bigg)^2\bigg[1.13+3.76\bigg(\frac{\alpha Z}{\beta}\bigg)^2\bigg]\]

where \(a_{TF}\) is the Thomas-Fermi screening length given by:

\[a_{TF}=\frac{0.88534\ a_0}{Z^{1/3}}\]

and \(a_0\) is the Bohr radius. \(R_{McF}\) is the ratio of the Mott to the Rutherford DCS given by McKinley and Feshbach approximation [MF48]:

\[R_{McF}=\bigg[1-\beta^2\sin^2(\theta/2) +Z\alpha\beta\pi\sin(\theta/2)\big(1- \sin(\theta/2)\big) \bigg]\]

The nuclear form factor for the exponential charge distribution is given by [BKMM02]:

\[F_N(q)=\Bigg[1+ \frac{(qR_N)^2}{12\hbar^2}\Bigg]^{-2}\]

where \(R_N\) is the nuclear radius that is parameterized by:

\[R_N=1.27A^{0.27}\ \textrm{fm}.\]

\(q\) is the momentum transferred to the nucleus and it is calculated as:

\[qc=\sqrt{T(T+2Mc^2)}\]

where \(T\) is the kinetic energy transferred to the nucleus. This kinetic energy is calculated in the GetNewDirection() method as:

\[T=\frac{2Mc^2(p'c)^2}{E_{cm}^2}\sin^2\theta/2.\]

The scattering angle \(\theta\) calculation is performed in the GetScatteringAngle() method of G4ScreeningMottCrossSection class. By means of AngleDistribution() function the scattering angle is chosen randomly according to the total cross section distribution (p.d.f. probability density function) by means of the inverse transform method.

In the SampleSecondary() method of G4eSingleScatteringModel the kinetic energy of the incident particle after scattering is then calculated as \(E'_{new}=E'-T\) where \(E'\) is the electron incident kinetic energy (in lab.); in addition the new particle direction and momentum are obtained from the scattering angle information.

Implementation Details

The scattering angle probability density function \(f(\theta)\) (p.d.f.) is performed by the AngleDistribution() of G4ScreeningMottCrossSection class where the inverse transform method is applied. The normalized cumulative function of the cross section is calculated as a function of the scattering angle in this way:

\[\sigma_n(\theta)\equiv \int f(\theta) d\theta=\frac{2\pi}{\sigma_{tot}}\int_{0}^{\theta} \frac{d\sigma(t)}{{d\Omega}}\sin t dt\]

The normalized cumulative function \(\sigma_n(\theta)\) depends on the DCS and its values range in the interval [0;1]. After this calculation a random number \(r\), uniformly distributed in the same interval [0;1], is chosen in order to fix the cumulative function value (i.e. \(r\equiv\sigma_n(\theta)\)). This number is the probability to find the scattering angle in the interval [\(\theta\); \(\theta+d\theta\)]. The scattering angle \(\theta\) is then given by the inverse function of \(\sigma_n(\theta)\). The threshold energy for displacement Th can by set by the user in her/his own Physics class by adding the electromagnetic model:

G4eSingleCoulombScatteringModel* mod =
  new G4eSingleCoulombScatteringModel();
mod->SetRecoilThreshold(Th);

If the energy lost by the incident particle is grater then this threshold value a new secondary particle is created for transportation processes. The energy lost is added to ProposeNonIonizingEnergyDeposit(). NIEL calculation is available in test58.

Bibliography

BKMM02(1,2)

A.V. Butkevich, R.P. Kokoulin, G.V. Matushko, and S.P. Mikheyev. Comments on multiple scattering of high-energy muons in thick layers. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 488(1-2):282–294, aug 2002. URL: https://doi.org/10.1016/S0168-9002(02)00478-3, doi:10.1016/s0168-9002(02)00478-3.

eal12(1,2,3,4)

M. J. Boschini et al. NUCLEAR AND NON-IONIZING ENERGY-LOSS OF ELECTRONS WITH LOW AND RELATIVISTIC ENERGIES IN MATERIALS AND SPACE ENVIRONMENT. In Astroparticle, Particle, Space Physics, Radiation Interaction, Detectors and Medical Physics Applications, pages 961–982. WORLD SCIENTIFIC, sep 2012. URL: https://doi.org/10.1142/9789814405072_0147, doi:10.1142/9789814405072_0147.

eal11(1,2,3,4,5)

M.J. Boschini et al. Nuclear and non-ionizing energy-loss for coulomb scattered particles from low energy up to relativistic regime in space radiation environment. In Cosmic Rays for Particle and Astroparticle Physics, 9–23. WORLD SCIENTIFIC, jun 2011. IBSN: 978-981-4329-02-6; arXiv 1011.4822. URL: https://doi.org/10.1142/9789814329033_0002, doi:10.1142/9789814329033_0002.

eal13(1,2)

M.J. Boschini et al. An expression for the mott cross section of electrons and positrons on nuclei with z up to 118. Radiation Physics and Chemistry, 90:39–66, sep 2013. URL: https://doi.org/10.1016/j.radphyschem.2013.04.020, doi:10.1016/j.radphyschem.2013.04.020.

LR07

C. Leroy and P.-G. Rancoita. Particle interaction and displacement damage in silicon devices operated in radiation environments. Reports on Progress in Physics, 70(4):493–625, mar 2007. URL: https://doi.org/10.1088/0034-4885/70/4/R01, doi:10.1088/0034-4885/70/4/r01.

LR11(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18)

C. Leroy and P.G. Rancoita. Principles of Radiation Interaction in Matter and Detection. World Scientific (Singapore), 3rd edition edition, 2011.

LQZ95(1,2,3)

Teng Lijian, Hou Qing, and Luo Zhengming. Analytic fitting to the mott cross section of electrons. Radiation Physics and Chemistry, 45(2):235–245, feb 1995. URL: https://doi.org/10.1016/0969-806X(94)00063-8, doi:10.1016/0969-806x(94)00063-8.

MF48(1,2,3,4,5,6,7)

William A. McKinley and Herman Feshbach. The coulomb scattering of relativistic electrons by nuclei. Physical Review, 74(12):1759–1763, dec 1948. URL: https://doi.org/10.1103/PhysRev.74.1759, doi:10.1103/physrev.74.1759.

Moliere48(1,2)

G. Molière. Theorie der Streuung schneller geladener Teilchen II. Mehrfach- und Vielfachstreuung. Zeitschrift Naturforschung Teil A, 3:78–97, February 1948. doi:10.1515/zna-1948-0203.

VJV87

H. De Vries, C.W. De Jager, and C. De Vries. Nuclear charge-density-distribution parameters from elastic electron scattering. Atomic Data and Nuclear Data Tables, 36(3):495–536, may 1987. URL: https://doi.org/10.1016/0092-640X(87)90013-1, doi:10.1016/0092-640x(87)90013-1.

ZO64

Elmar Zeitler and Haakon Olsen. Screening effects in elastic electron scattering. Physical Review, 136(6A):A1546–A1552, dec 1964. URL: https://doi.org/10.1103/PhysRev.136.A1546, doi:10.1103/physrev.136.a1546.