Single Scattering, Screened Coulomb Potential and NIEL

An alternative model of Coulomb scattering of ions have been developed based on [eal11] and references therein. The advantage of this model is the wide applicability range in energy from 50 keV to 100V TeV per nucleon.

Nucleus–Nucleus Interactions

As discussed in Ref. [eal11], at small distances from the nucleus, the potential energy is a Coulomb potential, while, at distances larger than the Bohr radius, the nuclear field is screened by the fields of atomic electrons. The interaction between two nuclei is usually described in terms of an interatomic Coulomb potential (e.g., see Section 2.1.4.1 of Ref. [LR09] and Section 4.1 of Ref. [eal93]), which is a function of the radial distance \(r\) between the two nuclei

(63)\[ V(r)=\frac{zZ e^2}{r}\, \,\Psi_{\rm I}(r_{\rm r}),\]

where \(ez\) (projectile) and \(eZ\) (target) are the charges of the bare nuclei, \(\Psi_{\rm I}\) is the interatomic screening function, and \(r_{\rm r}\) is given by

\[r_{\rm r}=\frac{r}{\rm {a_{I}}},\]

with \(\rm {a_{I}}\) the screening length (also termed screening radius). In the framework of the Thomas–Fermi model of the atom (e.g., see Ref. [eal11] and references therein), and thus following the approach of ICRU Report 49 [eal93], a commonly used screening length for \(z=1\) incoming particles is that from Thomas–Fermi

(64)\[ {\rm {a_{TF}}}=\frac{C_{\rm TF} \,{\rm {a_{0}}} }{Z^{1/3}},\]

and, for incoming particles with \(z \geq 2\), that introduced by Ziegler et al. [JFZL85] (and termed universal screening length):

(65)\[ {\rm {a_{U}}} = \frac{C_{\rm TF} \,{\rm {a_{0}}}}{z^{0.23}+Z^{0.23}},\]

where

\[{\rm {a_{0}}} =\frac{\hbar^2}{m e^2}\]

is the Bohr radius, \(m\) is the electron rest mass and

\[C_{\rm TF} = \frac{1}{2}\left(\frac{3 \, \pi}{4} \right)^{2/3} \simeq 0.88534\]

is a constant introduced in the Thomas–Fermi model.

The simple scattering model due to Wentzel [Wen26], with a single exponential screening function \(\Psi_{\rm I}(r_{\rm r})\) (e.g., see Ref. [eal11] and references therein), was repeatedly employed in treating single and multiple Coulomb-scattering with screened potentials. The resulting elastic differential cross section differs from the Rutherford differential cross section by an additional term, the screening parameter, which prevents the divergence of the cross section when the angle \(\theta\) of scattered particles approaches \(0^\circ\). The screening parameter \(A_{\rm s}\) (e.g., see Eq. (21) of [Bet53]) as derived by Molière [Moliere47][Moliere48] for the single Coulomb scattering using a Thomas–Fermi potential is expressed as

(66)\[A_{\rm s}=\left(\frac{\hbar}{2\,p\ a_{\rm I}}\right)^2\left[1.13+3.76 \times \left(\frac{\alpha zZ}{\beta}\right)^2\right].\]

\(a_{\rm I}\) is the screening length from Eqs.(64) – (65) for particles with \(z =1\) and \(z \geq 2\), respectively; \(\alpha\) is the fine-structure constant; \(p\) \(\beta c\) is the momentum (velocity) of the incoming particle undergoing the scattering onto a target supposed to be initially at rest; \(c\) and \(\hbar\) are the speed of light and the reduced Planck constant, respectively. When the (relativistic) mass, corresponding to rest mass \(m\), of the incoming particle is much lower than the rest mass \(M\) of the target nucleus, the differential cross section obtained from the Wentzel–Molière treatment of the single scattering is:

(67)\[\frac{d\sigma^{\rm WM}(\theta)}{d\Omega} = \left(\frac{zZe^2}{2\,p \, \beta c }\right)^2\frac{1}{\left[A_{\rm s}+\sin^2({\theta}/2)\right]^2}.\]

Equation (67) differs from Rutherford’s formula, as already mentioned, for the additional term \(A_{\rm s}\) to \(\sin^2({\theta}/2)\). As discussed in Ref. [eal11], for \(\beta \simeq 1\) (i.e., at very large \(p\)) and with \(A_{\rm s}\ll 1\), one finds that the cross section approaches a constant:

(68)\[\sigma^{\rm WM}_{\rm c} \simeq \left(\frac{2\, zZe^2 a_{\rm I}}{\hbar c }\right)^2\frac{ \pi }{1.13+3.76 \times \left(\alpha zZ\right)^2 }.\]

As discussed in Ref. [eal11] and references therein, for a scattering under the action of a central potential (for instance that due to a screened Coulomb field), when the rest mass of the target particle is no longer much larger than the relativistic mass of the incoming particle, the expression of the differential cross section must properly be re-written in the center of mass system in terms of an “effective particle” with momentum equal to that of the incoming particle (\(p'_{in}\)) and rest mass equal to the relativistic reduced mass

(69)\[\mu_{\rm rel} = \frac{m M }{M_{1,2}}.\]

\(M_{1,2}\) is the invariant mass; \(m\) and \(M\) are the rest masses of the incoming and target particles, respectively. The “effective particle” velocity is given by:

\[\beta_{\rm r} c = c \sqrt{\left[1+ \left(\frac{\mu_{\rm rel} c}{p'_{in} } \right)^2 \right]^{-1}}.\]

Thus, one finds (e.g, see Ref. [eal11]):

(70)\[ \frac{d\sigma^{\rm WM}(\theta')}{d\Omega'} = \left(\frac{zZe^2}{2\,p'_{in} \, \beta_{\rm r} c }\right)^2\frac{1}{\left[A_{\rm s}+\sin^2({\theta'}/2)\right]^2},\]

with

(71)\[A_{\rm s}=\left(\frac{\hbar}{2\,p'_{in}\ a_{\rm I}}\right)^2\left[1.13+3.76 \times \left(\frac{\alpha zZ}{\beta_{\rm r}}\right)^2\right]\]

and \(\theta'\) the scattering angle in the center of mass system.

The energy \(T\) transferred to the recoil target is related to the scattering angle as \(T=T_{max}\sin^2{(\theta'/2)}\), where \(T_{max}\) is the maximum energy which can be transferred in the scattering (e.g., see Section 1.5 of Ref. [LR09]), thus, assuming an isotropic azimuthal distribution one can re-write Eq.(70) in terms of the kinetic recoil energy \(T\) of the target

(72)\[ \frac{d\sigma^{\rm WM}(T)}{dT} = \pi \left(\frac{zZe^2}{p'_{in} \, \beta_{\rm r} c }\right)^2\frac{T_{max}}{\left[T_{max}\, A_{\rm s}+T\right]^2}.\]

Furthermore, one can demonstrate that Eq.(72) can be re-written as (e.g, see Ref. [eal11]);

(73)\[ \frac{d\sigma^{\rm WM}(T)}{dT} = 2\, \pi \left({zZe^2}\right)^2 \frac{ E^2}{p^2 M c^4}\, \frac{1}{\left[T_{max}\, A_{\rm s}+T\right]^2}\]

with \(p\) and \(E\) the momentum and total energy of the incoming particle in the laboratory. Equation (73) expresses, as already mentioned, the differential cross section as a function of the (kinetic) energy \(T\) achieved by the recoil target.

Nuclear Stopping Power

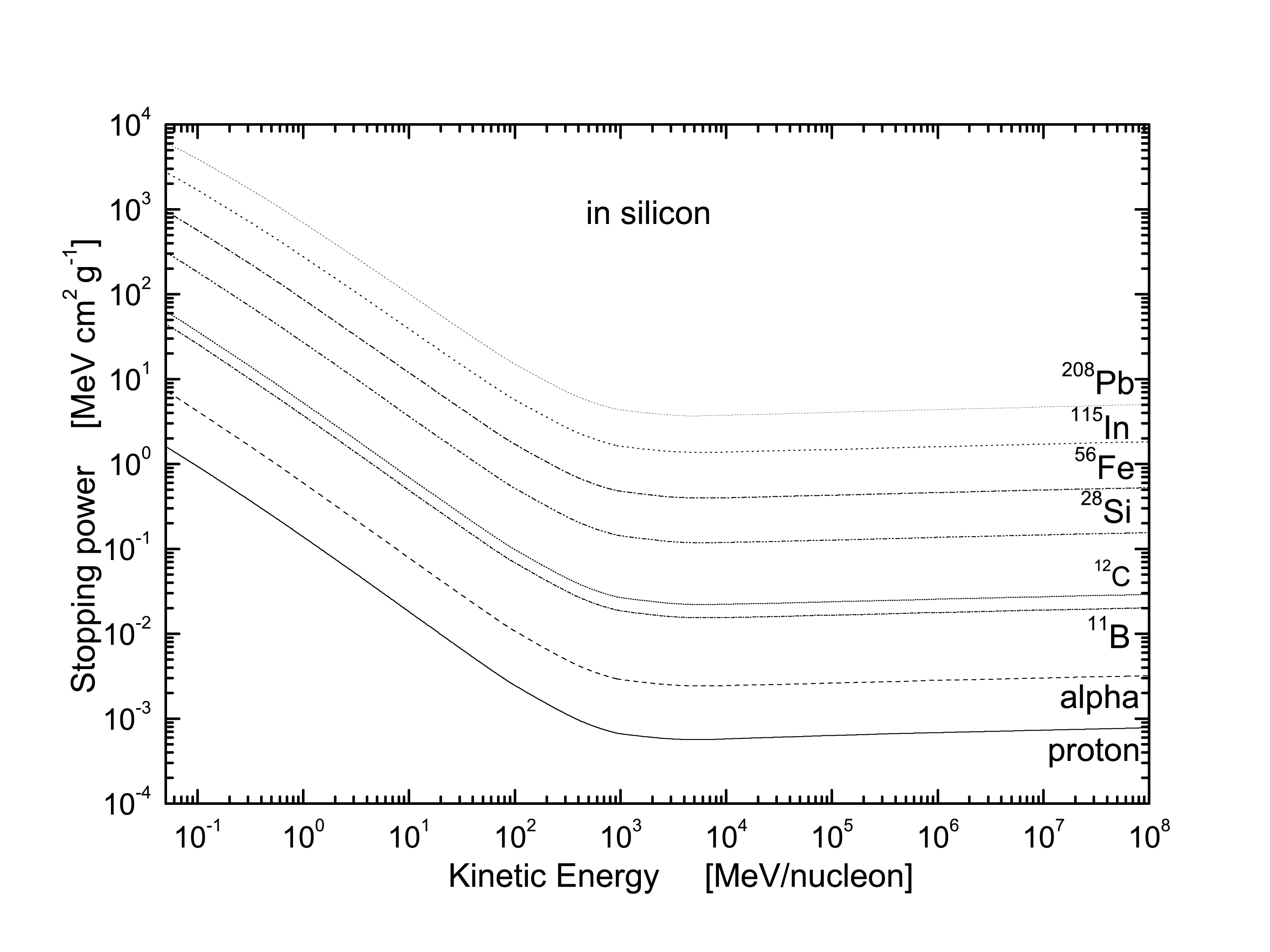
Fig. 19 Nuclear stopping power from Ref. [eal11] in MeV cm ² g ^-1 calculated using Eq.(74) in silicon shown as a function of the kinetic energy per nucleon from 50 keV/nucleon up 100 TeV/nucleon for protons, \(\alpha\)-particles and ¹¹B, ¹²C, ²⁸Si, ⁵⁶Fe, ¹¹⁵In, ²⁰⁸Pb nuclei.

Using Eq. (73), the nuclear stopping power in MeVcm\(^{-1}\) is obtained as

(74)\[- \left(\frac{dE}{dx}\right)_{\rm nucl} = 2\, {n_A} \pi \left({zZe^2}\right)^2 \frac{ E^2}{p^2 M c^4}\!\left[\frac{A_{\rm s}}{A_{\rm s}+1}-1+\ln\left(\!\frac{A_{\rm s}+1}{A_{\rm s}}\!\right)\right].\]

\(n_A\) is the number of nuclei (atoms) per unit of volume and, the negative sign indicates that the energy is lost by the incoming particle. As discussed in Ref. [eal11], a slight increase of the nuclear stopping power with energy is expected because of the decrease of the screening parameter with energy.

For instance, in Fig. 19 the nuclear stopping power in silicon is shown as a function of the kinetic energy per nucleon for protons, \(\alpha\)-particles and ¹¹B, ¹²C, ²⁸Si, ⁵⁶Fe, ¹¹⁵In, ²⁰⁸Pb nuclei.

A comparison of the present treatment with that obtained from Ref. [JFZL85], available in SRIM (2008) [JFZ08], using the universal screening potential (see also Ref. [ZBZ08]) is discussed in Ref. [eal11]: a good agreement is achieved down to about 150 keV/nucleon. At large energies, the non-relativistic approach due to Ref. [JFZL85] becomes less appropriate and deviations from stopping powers calculated by means of the universal screening potential are expected and observed.

The non-relativistic approach based on the universal screening potential of [JFZL85] was also used by ICRU (1993) [eal93] to calculate nuclear stopping powers due to protons and \(\alpha\)-particles in materials. ICRU (1993) used as screening lengths those from Eqs.(64) for protons and (65) for \(\alpha\)-particles, respectively. As discussed in Ref. [eal11], the stopping powers for protons (\(\alpha\)-particles) from Eq.(74) are less than \(\approx 5\)% larger than those reported by ICRU (1993) [eal93] from 50 keV/nucleon up to \(\approx 8\)MeV (19 MeV/nucleon). At larger energies the stopping powers from Eq.(74) differ from those from ICRU, as expected, due to the complete relativistic treatment of the present approach (see Ref. [eal11]).

The simple screening parameter used so far (Eq.(71)), derived by Molière [Moliere47]), can be modified by means of a practical correction, i.e.,

(75)\[A_{\rm s}'=\left(\frac{\hbar}{2\,p'_{in}\ a_{\rm I}}\right)^2\left[1.13+3.76 \times C \left(\frac{\alpha zZ}{\beta_{\rm r}}\right)^2\right],\]

to achieve a better agreement with low energy calculations of [JFZL85]. For instance, as discussed in Ref. [eal11], for \(\alpha\)-particles and heavier ions, with

(76)\[C = \left( 10 \pi z Z \alpha \right)^{0.12}\]

the stopping powers obtained from Eq.(74) (in which \(A_{\rm s}'\) replaces \(A_{\rm s}\)) differ from the values of SRIM (2008) by less than \(\approx 4.7\) (3.6)% for \(\alpha\)-particles (lead ions) in silicon down to about 50 keV/nucleon. With respect to the tabulated values of ICRU (1993), the agreement for \(\alpha\)-particles is usually better than 4% at low energy down to 50 keV/nucleon. A 5% agreement is achieved at about 50 keV/nucleon in case of a lead medium. At very high energy, the stopping power is slightly affected when \(A_{\rm s}'\) replaces \(A_{\rm s}\) (Ref. [eal11]).

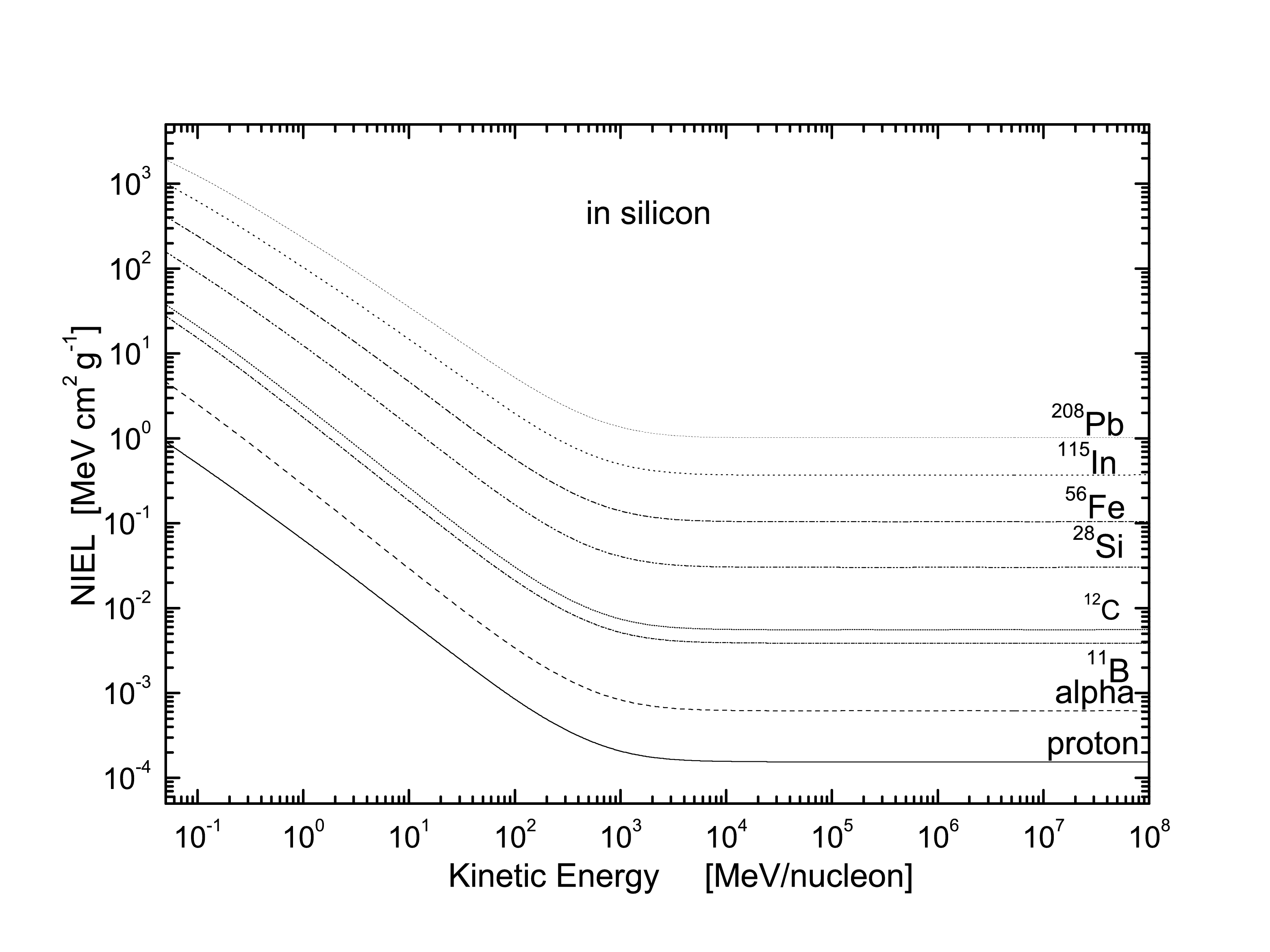
Fig. 20 Non-ionizing stopping power from Ref. [eal11] calculated using Eq.(77) in silicon is shown as a function of the kinetic energy per nucleon, from 50 keV/nucleon up 100 TeV/nucleon, for protons, \(\alpha\)-particles and ¹¹B, ¹²C, ²⁸Si, ⁵⁶Fe, ¹¹⁵In, ²⁰⁸Pb nuclei. The threshold energy for displacement is 21 eV in silicon.

Non-Ionizing Energy Loss due to Coulomb Scattering

A relevant process which causes permanent damage to the silicon bulk structure is the displacement damage (e.g., see Chapter 4 of Ref. [LR09], Ref. [LR07] and references therein). Displacement damage may be inflicted when a primary knocked-on atom (PKA) is generated. The interstitial atom and relative vacancy are termed a Frenkel pair (FP). In turn, the displaced atom may have sufficient energy to migrate inside the lattice and, by further collisions, can displace other atoms as in a collision cascade. This displacement process modifies the bulk characteristics of the device and causes its degradation. The total number of FPs can be estimated calculating the energy density deposited from displacement processes. In turn, this energy density is related to the Non-Ionizing Energy Loss (NIEL), i.e., the energy per unit path lost by the incident particle due to displacement processes.

In case of Coulomb scattering on nuclei, the non-ionizing energy loss can be calculated using the Wentzel–Molière differential cross section (Eq.(73)) discussed in Single Scattering, Screened Coulomb Potential and NIEL, i.e.,

(77)\[- \left(\frac{dE}{dx}\right)_{\rm nucl}^{\rm NIEL} = n_A\,\int^{T_{max}}_{T_d} \!T\,L(T)\,\frac{d\sigma^{\rm WM}(T)}{dT}\,dT\ ,\]

where \(E\) is the kinetic energy of the incoming particle, \(T\) is the kinetic energy transferred to the target atom, \(L(T)\) is the fraction of \(T\) deposited by means of displacement processes. The expression of \(L(T)\), denoted the Lindhard partition function, can be found, for instance, in Equations (4.94, 4.96) of Section 4.2.1.1 in Ref. [LR09] and references therein. \(T_{\rm de}= T\, L(T)\) is the damage energy, i.e., the energy deposited by a recoil nucleus with kinetic energy \(T\) via displacement damages inside the medium. The integral in Eq.(77) is computed from the minimum energy \(T_d\), denoted the threshold energy for displacement, i.e., that energy necessary to displace the atom from its lattice position, up to the maximum energy \(T_{max}\) that can be transferred during a single collision process. \(T_d\) is about 21 eV in silicon. For instance, in Fig. 20 the non-ionizing energy loss in silicon is shown as a function of the kinetic energy per nucleon for protons, \(\alpha\)-particles and ¹¹B, ¹²C, ²⁸Si, ⁵⁶Fe, ¹¹⁵In, ²⁰⁸Pb nuclei.

A further discussion on the agreement with the results obtained by Jun et al. [eal03], using a relativistic treatment of Coulomb scattering of protons with kinetic energies from 50 MeV to 1 GeV on silicon, can be found in Ref. [eal11].

G4IonCoulombScatteringModel

As discussed so far, high energy particles may inflict permanent damage to the electronic devices employed in a radiation environment. In particular the nuclear energy loss is important for the formation of defects in semiconductor devices. Nuclear energy loss is also responsible for the displacement damage which is the typical cause of degradation for silicon devices. The electromagnetic model G4IonCoulombScatteringModel was created in order to simulate the single scattering of protons, alpha particles and all heavier nuclei incident on all target materials in the energy range from 50–100 keV/nucleon to 10 TeV.

The Method

The differential cross section previously described is calculated by means of the class G4IonCoulombCrossSection where a modified version of the Wentzel’s cross section is used. To solve the scattering problem of heavy ions it is necessary to introduce an effective particle whose mass is equal to the relativistic reduced mass of the system defined as

\[\mu_r\equiv\frac{m_1m_2c^2}{E_{cm}}.\]

\(m_1\) and \(m_2\) are the incident and target rest masses respectively, and \(E_{cm}\) (in Eq.(69), \(M_{1,2}=E_{cm}/c^2\)) is the total center of mass energy of the two particle system. The effective particle interacts with a fixed scattering center with interacting potential expressed by Eq.(63). The momentum of the effective particle is equal to the momentum of the incoming particle calculated in the center of mass system (\(\textbf{p}_r\equiv\textbf{p}_{1cm}\)). Since the target particle is inside the material it can be considered at rest in the laboratory, and as a consequence the magnitude of \(\textbf{p}_r\) is calculated as

\[p_r\equiv p_{1cm} =p_{1lab}\frac{m_2c^2}{E_{cm}},\]

with \(E_{cm}\) given by

(78)\[E_{cm}=\sqrt{(m_1c^2)^2+(m_2c^2)^2+2E_{1lab}m_2c^2},\]

where \(p_{1lab}\) is the momentum, and \(E_{1lab}\) the total energy, of the incoming particle in the laboratory system. The velocity \(\beta_r\) of the effective particle is obtained by the relation

\[\frac{1}{\beta_r^2}=1+\Bigg(\frac{\mu_rc^2}{p_rc}\Bigg)^2.\]

The modified Wentzel’s cross section is then equal to:

(79)\[\frac{d\sigma(\theta_r)}{d\Omega}=\bigg(\frac{Z_1Z_2e^2}{p_rc\ \beta_r}\bigg)^2\frac{1}{(2A_s+1-\cos{\theta_r})^2}\]

(in Eq.(70)) \(p'_{in}\equiv p_r \) where \(Z_1\) and \(Z_2\) are the nuclear proton numbers of projectile and of target respectively; \(A_s\) is the screening coefficient (see Eq.(71)) and \(\theta_r\) is the scattering angle of the effective particle which is equal to the one in the center of mass system (\(\theta_r\equiv\theta_{1cm}\)). Knowing the scattering angle, the recoil kinetic energy of the target particle after scattering is calculated by

(80)\[T =m_2c^2\Bigg(\frac{p_{1lab}c}{E_{cm}}\Bigg)^2(1-\cos{\theta_r}).\]

The momentum and the total energy of the incident particle after scattering in the laboratory system are obtained by the usual Lorentz transformations.

Implementation Details

In the G4IonCoulombScatteringModel the scattering off electrons is not considered: only scattering off nuclei is simulated. Secondary particles are generated when \(T\) of Eq.(80) is greater than a given threshold for displacement \(T_d\); it is not cut in range. The user can set this energy threshold \(T_d\) by the method SetRecoilThreshold(G4double Td). The default screening coefficient \(A_s\) is given by Eq.(71). If the user wants to use the one given by Eq.(75) the condition SetHeavyIonCorr(1) must be set. When \(Z_1=1\), the Thomas-Fermi screening length (\(a_{TF}\) of Eq. (64)) is used in the calculation of \(A_s\). For \(Z_1\geq 2\) the screening length is the universal one (\(a_U\) of Eq. (65)). In the G4IonCoulombCrossSection the total differential cross section is obtained by the method NuclearCrossSection() where the Eq.(79) is integrated in the interval (0, \(\pi\)):

(81)\[\sigma=\pi\bigg(\frac{Z_1Z_2e^2}{p_rc\ \beta_r}\bigg)^2\frac{1}{A_s(A_s+1)}\]

The cosine of the scattering angle is chosen randomly in the interval (-1, 1) according to the distribution of the total cross section and it is given by the method SampleCosineTheta() which returns (\(1-\cos{\theta_r}\)).

Bibliography

Bet53

H.A. Bethe. Phys. Rev., 89:1256, 1953.

eal03

Insoo Jun et al. Proton nonionizing energy loss (niel) for device applications. IEEE Transactions on Nuclear Science, 50(6):1924–1928, dec 2003. URL: https://doi.org/10.1109/TNS.2003.820760, doi:10.1109/tns.2003.820760.

eal93(1,2,3,4)

M.J. Berger et al. Report 49. Journal of the International Commission on Radiation Units and Measurements, os25(2):NP–NP, may 1993. ICRU Report 49. URL: https://doi.org/10.1093/jicru/os25.2.Report49, doi:10.1093/jicru/os25.2.report49.

eal11(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17)

M.J. Boschini et al. Nuclear and non-ionizing energy-loss for coulomb scattered particles from low energy up to relativistic regime in space radiation environment. In Cosmic Rays for Particle and Astroparticle Physics, 9–23. WORLD SCIENTIFIC, jun 2011. IBSN: 978-981-4329-02-6; arXiv 1011.4822. URL: https://doi.org/10.1142/9789814329033_0002, doi:10.1142/9789814329033_0002.

JFZL85(1,2,3,4,5)

J.P. Biersack J.F. Ziegler and U. Littmark. The Stopping Range of Ions in Solids. Pergamon Press (New York), vol. 1 edition, 1985.

JFZ08

J.P. Biersack J.F. Ziegler, M.D. Ziegler. The stopping and range of ions in matter, \em SRIM version 2008.03 (2008). http://www.srim.org/, 2008. [Online; accessed 26-october-2017].

LR07

C. Leroy and P.-G. Rancoita. Particle interaction and displacement damage in silicon devices operated in radiation environments. Reports on Progress in Physics, 70(4):493–625, mar 2007. URL: https://doi.org/10.1088/0034-4885/70/4/R01, doi:10.1088/0034-4885/70/4/r01.

LR09(1,2,3,4)

C. Leroy and P.G. Rancoita. Principles of Radiation Interaction in Matter and Detection. World Scientific (Singapore), 2nd edition edition, 2009.

Moliere47(1,2)

G. Molière. Zeitschrift Naturforschung Teil A, 2:133–145, 1947.

Moliere48

G. Molière. Theorie der Streuung schneller geladener Teilchen II. Mehrfach- und Vielfachstreuung. Zeitschrift Naturforschung Teil A, 3:78–97, February 1948. doi:10.1515/zna-1948-0203.

Wen26

G. Wentzel. Zwei bemerkungen über die zerstreuung korpuskularer strahlen als beugungserscheinung. Zeitschrift für Physik, 40(8):590–593, aug 1926. URL: https://doi.org/10.1007/BF01390457, doi:10.1007/bf01390457.

ZBZ08

James F Ziegler, Jochen P Biersack, and Matthias D Ziegler. SRIM: the stopping and range of ions in matter. Cadence Design Systems, Raleigh, NC, 2008. URL: https://cds.cern.ch/record/1525729.